题目内容
7.若$a=\int_0^2{xdx}$,则二项式${(x-\frac{a+1}{x})^6}$展开式中的常数项是( )| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
分析 求定积分得a的值,再利用二项式展开式的通项公式求出展开式的常数项.
解答 解:$a=\int_0^2{xdx}$=$\frac{1}{2}$x2${|}_{0}^{2}$=$\frac{1}{2}$×22=2,
∴二项式${(x-\frac{a+1}{x})^6}$=${(x-\frac{3}{x})}^{6}$展开式中,
通项公式为Tr+1=${C}_{6}^{r}$•x6-r•${(-\frac{3}{x})}^{r}$=(-3)r•${C}_{6}^{r}$•x6-2r,
令6-2r=0,解得r=3;
∴展开式的常数项为:
T4=(-3)3•${C}_{6}^{3}$=-540.
故选:C.
点评 本题考查了定积分的计算问题,也考查了二项式展开式的通项公式应用问题,是基础题.

练习册系列答案
相关题目
18.锐角三角形ABC的三边长a,b,c成等差数列,且a2+b2+c2=21,则实数b的取值范围是( )
| A. | $({\sqrt{6},\sqrt{7}}]$ | B. | $({0,\sqrt{7}}]$ | C. | $({\frac{{2\sqrt{42}}}{5},\sqrt{7}}]$ | D. | (6,7] |
19.数列{an}中,若存在ak,使得“ak>ak-1且ak>ak+1”成立(其中k≥2,k∈N*),ak则称为{an}的一个H值.现有如下数列:
①an=1-2n
②an=sinn
③an=$\frac{n-2}{{e}^{n-3}}$
④an=lnn-n
则存在H值的数列的序号为( )
①an=1-2n
②an=sinn
③an=$\frac{n-2}{{e}^{n-3}}$
④an=lnn-n
则存在H值的数列的序号为( )
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
16.${log_2}8+{log_2}\frac{1}{2}$=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
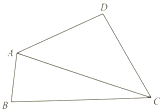 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.