题目内容
15.已知a,b,c分别为△ABC三个内角A、B、C的对边,c=2,且(2+b)(sinC-sinB)=a(sinA-sinB).(Ⅰ)求∠C的大小;
(Ⅱ)求△ABC周长l的最大值.
分析 (I)由c=2,且(2+b)(sinC-sinB)=a(sinA-sinB).由正弦定理可得:(c+b)(c-b)=a(a-b),化为:a2+b2-c2=ab.再利用余弦定理即可得出C.
(II)由(I)可得:A+B=$\frac{2π}{3}$.可得B=$\frac{2π}{3}$-A$(0<A<\frac{2π}{3})$.由正弦定理可得:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{2}{sin\frac{π}{3}}$=$\frac{4\sqrt{3}}{3}$.可得a=$\frac{4\sqrt{3}}{3}$sinA,b=$\frac{4\sqrt{3}}{3}$sinB.可得a+b+c=$\frac{4\sqrt{3}}{3}$sinA+$\frac{4\sqrt{3}}{3}$sinB+2=4sin$(A+\frac{π}{6})$+2.即可得出.
解答 解:(I)由c=2,且(2+b)(sinC-sinB)=a(sinA-sinB).
由正弦定理可得:(c+b)(c-b)=a(a-b),化为:a2+b2-c2=ab.
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,C∈(0,π).
∴C=$\frac{π}{3}$.
(II)由(I)可得:A+B=$\frac{2π}{3}$.
∴B=$\frac{2π}{3}$-A$(0<A<\frac{2π}{3})$.
由正弦定理可得:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{2}{sin\frac{π}{3}}$=$\frac{4\sqrt{3}}{3}$.
∴a=$\frac{4\sqrt{3}}{3}$sinA,b=$\frac{4\sqrt{3}}{3}$sinB.
∴a+b+c=$\frac{4\sqrt{3}}{3}$sinA+$\frac{4\sqrt{3}}{3}$sinB+2
=$\frac{4\sqrt{3}}{3}$[sinA+sin($\frac{2π}{3}$-A)]+2
=$\frac{4\sqrt{3}}{3}$($\frac{3}{2}$sinA+$\frac{\sqrt{3}}{2}$cosA)+2
=4sin$(A+\frac{π}{6})$+2.
故当A+$\frac{π}{6}$=$\frac{π}{2}$时,△ABC周长l的最大值为6.
点评 本题考查了正弦定理、余弦定理、和差公式、三角函数的单调性、三角形内角和定理,考查了推理能力与计算能力,属于中档题.

∈[-4,-2)时,f(x)≥t2-$\frac{7}{3}$t恒成立,则实数t的取值范围是( )
| A. | [$\frac{1}{2}$,3) | B. | (-∞,$\frac{1}{2}$]∪(3,+∞) | C. | [$\frac{1}{3}$,2] | D. | (-∞,$\frac{1}{3}$]∪[2,+∞) |
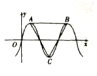 函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )| A. | $\frac{9}{2}$ | B. | $\frac{{9\sqrt{3}}}{2}$ | C. | $9\sqrt{3}+1$ | D. | $\frac{{9({\sqrt{3}+1})}}{2}$ |
| 月利润(单位:千万元) | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
| 频数 | 2 | 1 | 2 | 4 | 1 |
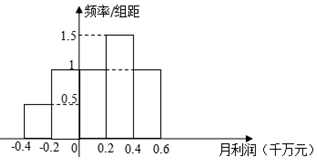
(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\frac{5}{3}$ |
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
| A. | ?x<0,x3≥0 | B. | ?x0>0,x03≤0 | C. | ?x0<0,x03≥0 | D. | ?x>0,x3≥0 |
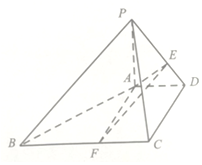 如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD
如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD