题目内容
16.${log_2}8+{log_2}\frac{1}{2}$=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用对数性质及运算法则直接求解.
解答 解:${log_2}8+{log_2}\frac{1}{2}$=$lo{g}_{2}(8×\frac{1}{2})$=log24=2.
故选:A.
点评 本题考查对数值的求法,是基础题,解题时要认真审题,注意对数性质及运算法则的合理运用.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
6.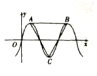 函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
 函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )| A. | $\frac{9}{2}$ | B. | $\frac{{9\sqrt{3}}}{2}$ | C. | $9\sqrt{3}+1$ | D. | $\frac{{9({\sqrt{3}+1})}}{2}$ |
7.若$a=\int_0^2{xdx}$,则二项式${(x-\frac{a+1}{x})^6}$展开式中的常数项是( )
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
1.函数$y=\sqrt{\frac{x-3}{2-x}}$的定义域是( )
| A. | {x|2≤x≤3} | B. | {x|x≤2或x≥3} | C. | {x|2<x≤3} | D. | {x|x<2或x≥3} |
5.已知命题p:?x<0,x3<0,那么¬p是( )
| A. | ?x<0,x3≥0 | B. | ?x0>0,x03≤0 | C. | ?x0<0,x03≥0 | D. | ?x>0,x3≥0 |
6.在△ABC中,a,b,c分别为内角A,B,C的对边,且a2=3b2+3c2-2$\sqrt{3}$bcsinA,则C的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
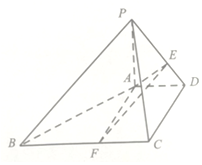 如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD
如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD