题目内容
12.设函数f(x)=|x+1|+x-m的最小值是-3.(1)求m的值;
(2)若$\frac{1}{a}+\frac{1}{b}=2$,是否存在正实数a,b满足$(a+1)(b+1)=\frac{7}{2}$?并说明理由.
分析 (1)化简函数为分段函数,利用函数的单调性求解函数的最小值,然后求解m即可.
(2)利用$\frac{1}{a}+\frac{1}{b}=2$,转化推出ab的范围,化简$(a+1)(b+1)=\frac{7}{2}$,推出ab的范围,即可得到结果.
解答 解:(1)因为$f(x)=|{x+1}|+x-m=\left\{\begin{array}{l}2x+1-m,x≥-1\\-1-m,x<-1\end{array}\right.$,x≥-1时,函数是增函数,
所以ymin=-1-m=-3⇒m=2.
(2)∵$\frac{1}{a}+\frac{1}{b}=2$,∴$a+b=2ab≥2\sqrt{ab}⇒ab≥1$,
∵$(a+1)(b+1)=a+b+ab+1=3ab+1=\frac{7}{2}$,
∴$ab=\frac{5}{6}<1$,矛盾.
所以不存在正实数a,b满足条件.
点评 本题考查分段函数的应用,函数的最值以及基本不等式的应用,考查计算能力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
2.若$\frac{1+cosα}{sinα}$=2,则cosα-3sinα=( )
| A. | -3 | B. | 3 | C. | -$\frac{9}{5}$ | D. | $\frac{9}{5}$ |
3.某渔业公司为了解投资收益情况,调查了旗下的养鱼场和远洋捕捞队近10个月的利润情况.根据所收集的数据得知,近10个月总投资养鱼场一千万元,获得的月利润频数分布表如下:
近10个月总投资远洋捕捞队一千万元,获得的月利润频率分布直方图如下:
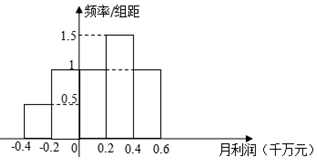
(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
| 月利润(单位:千万元) | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
| 频数 | 2 | 1 | 2 | 4 | 1 |

(Ⅰ)根据上述数据,分别计算近10个月养鱼场与远洋捕捞队的月平均利润;
(Ⅱ)公司计划用不超过6千万元的资金投资于养鱼场和远洋捕捞队,假设投资养鱼
场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元,且投资养鱼场的资金不少于投资远洋捕捞队的资金的2倍.试用调查数据,给出公司分配投资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
7.若$a=\int_0^2{xdx}$,则二项式${(x-\frac{a+1}{x})^6}$展开式中的常数项是( )
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
17.设不等式组$\left\{\begin{array}{l}{y≤x+1}\\{2x+y≤7}\\{x+2y≥5}\end{array}\right.$,表示的平面区域为D,若D中存在点在曲线y=ax2上,则实数a的取值范围是( )
| A. | [1,2] | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{6}$,2] | D. | [$\frac{1}{9}$,2] |
1.函数$y=\sqrt{\frac{x-3}{2-x}}$的定义域是( )
| A. | {x|2≤x≤3} | B. | {x|x≤2或x≥3} | C. | {x|2<x≤3} | D. | {x|x<2或x≥3} |
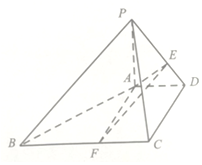 如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD
如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD