题目内容
7.假设小华和小明所在的班级共有50名学生,并且这50名学生早上到校先后的可能性是相同的.则小华比小明先到校的概率是$\frac{1}{2}$.分析 只需考虑小华、小明到校的顺序问题,2人到校的顺序共2种,且每种情况出现的可能性相同,故为古典概型.
解答 解:∵小华、小明早上到校先后的可能性是相同的,
∴小华比小明先到校的概率相等,
∴事件“小华比小明”的概率是$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查等可能事件的概率、古典概型等知识,属基本运算的考查.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点为F(c,0),若圆C:(x-c)2+y2=4a2与双曲线E的渐近线相切,则E的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
2.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取( )名学生.
| A. | 40 | B. | 50 | C. | 60 | D. | 70 |
12.若函数f(x)的导函数f′(x)=x(2-x)e-x,则下列关系一定成立的是( )
| A. | f(2)>0 | B. | f(0)>f(1) | C. | f(2)<f(1) | D. | f(2)>f(3) |
16.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
| 甲 | 29 | 37 | 35 | 33 | 26 | 50 |
| 乙 | 32 | 33 | 28 | 34 | 40 | 43 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
17.集合M={x|0≤x<2},集合N={x|x2+2x-3<0},则集合M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
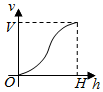
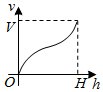
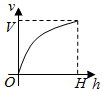
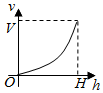
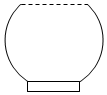 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )