题目内容
12．若函数f（x）的导函数f′（x）=x（2-x）e-x，则下列关系一定成立的是（ ）| A． | f（2）＞0 | B． | f（0）＞f（1） | C． | f（2）＜f（1） | D． | f（2）＞f（3） |
分析 根据导数判断出函数的单调性，再由函数的单调性判断即可．
解答 解：当f′（x）=x（2-x）e-x＞0，解得0＜x＜2，故f（x）单调递增，
当f′（x）=x（2-x）e-x＜0，解得x＜或x＞2，故f（x）单调递减，
∴f（2）＞f（3）
故选：D．
点评 本题考查了导数和函数的单调性的关系，属于基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
2．某市交管部门随机抽取了89位司机调查有无酒驾习惯，汇总数据的如表：
已知在这89人随机抽取1人，抽到无酒驾习惯的概率为$\frac{57}{89}$，
（1）将如表中空白部分数据补充完整；
（2）若从有酒驾习惯的人中按性别用分层抽样的方法抽取8人参加某项活动，现从这8人中随机抽取2人，记抽到女性的人数为X，求X得分布列和数学期望．
| 男性 | 女性 | 合计 | |
| 无酒驾习惯 | 31 | ||
| 有酒驾习惯 | 8 | ||
| 合计 | 89 |
（1）将如表中空白部分数据补充完整；
（2）若从有酒驾习惯的人中按性别用分层抽样的方法抽取8人参加某项活动，现从这8人中随机抽取2人，记抽到女性的人数为X，求X得分布列和数学期望．
3．命题“经过圆外一点与圆相切的直线至少有一条”的否定是（ ）
| A． | 经过圆外一点与圆相切的直线至多有两条 | |
| B． | 经过圆外一点与圆相切的直线有两条 | |
| C． | 经过圆外一点与圆相切的直线不存在 | |
| D． | 经过圆外一点与圆相切的直线至多有一条 |
20．下列叙述中正确的是（ ）
| A． | 若a，b，c∈R，则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” | |
| B． | 若a，b，c∈R，则“ab2＞cb2”的充要条件是“a＞c” | |
| C． | “直线a∥b”是“直线a⊥平面α，直线b⊥平面α”的必要条件 | |
| D． | b2=ac是a，b，c成等比数列的充要条件 |
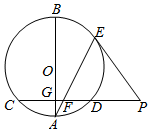如图，AB是圆O的一条直径，弦CD垂直于AB，垂足为点G，E是劣弧$\widehat{BD}$上一点，点E处的切线与CD的延长线交于点P，连接AE，交CD于点F．
1．
若如图程序执行的结果是10，则输入的x的值是（ ）
若如图程序执行的结果是10，则输入的x的值是（ ）| A． | 0 | B． | 10 | C． | -10 | D． | 10或-10 |
2．已知集合M={x|x＞0}，N={x|x2≤4}，则集合M∩N=（ ）
| A． | {x|-2＜x＜0} | B． | {x|0＜x≤2} | C． | {x|-2＜x＜2} | D． | {x|x＞-2} |