题目内容
正四棱锥的底面边长为2,侧棱长均为
,其正视图和侧视图是全等的等腰三角形,则正视图的周长为 .
| 3 |
考点:简单空间图形的三视图
专题:计算题
分析:几何体的主视图和侧视图是全等的等腰三角形,推知腰是正四棱锥的斜高,求出斜高,即可求出正视图的周长.
解答:
解:由于正四棱锥的底面边长为2,侧棱长为
,
其主视图和侧视图是全等的等腰三角形;
所以主视图和侧视图中的腰是正四棱锥的斜高.
其长为:
则正视图的周长:2+2
.
故答案是2+2
.
| 3 |
其主视图和侧视图是全等的等腰三角形;
所以主视图和侧视图中的腰是正四棱锥的斜高.
其长为:
| 2 |
则正视图的周长:2+2
| 2 |
故答案是2+2
| 2 |
点评:本题考查简单几何体的三视图,易错点是:主视图和侧视图是全等的等腰三角形中的腰是正四棱锥的斜高.

练习册系列答案
相关题目
先后抛掷一枚质地均匀的硬币3次,有2次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线y=mx+(2m+1)恒过一定点,则此点是( )
| A、(1,2) |
| B、(2,1) |
| C、(-2,1) |
| D、(1,-2) |
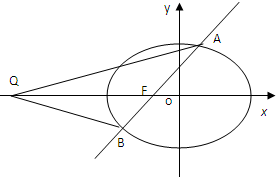 已知椭圆C:
已知椭圆C: