题目内容
直线
x-3y+2=0和直线
x+y-1=0的倾斜角分别为α，β，tan（α+β）=（ ）
| 3 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点：两角和与差的正切函数
专题：直线与圆
分析：由题意可得tanα=
，tanβ=-
，再根据tan（α+β）=
，计算求得结果．
| ||
| 3 |
| 3 |
| tanα+tanβ |
| 1-tanαtanβ |
解答：
解：∵直线
x-3y+2=0和直线
x+y-1=0的倾斜角分别为α，β，
∴tanα=
，tanβ=-
．
∴tan（α+β）=
=
=-
，
故选：B．
| 3 |
| 3 |
∴tanα=
| ||
| 3 |
| 3 |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
| ||||||
1-
|
| ||
| 3 |
故选：B．
点评：本题主要考查直线的倾斜角和斜率，两角和的正切公式的应用，属于中档题．
练习册系列答案
相关题目
若函数y=2x-2+3的图象恒过点P，则点P为（ ）
| A、（2，3） |
| B、（1，1） |
| C、（0，1） |
| D、（2，4） |
若16-x2≥0，则（ ）
| A、0≤x≤4 |
| B、-4≤x≤0 |
| C、-4≤x≤4 |
| D、x≤-4或x≥4 |
已知|
|=3，|
|=5，且
+λ
与
-λ
垂直，则λ等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、±
| ||
C、±
| ||
D、±
|
方程ax2+2x+1=0恰有一个负实根，则a的取值范围为（ ）
| A、a＜0 | B、a≤0 |
| C、a＞0 | D、a=0 |
先后抛掷一枚质地均匀的硬币3次，有2次正面朝上的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
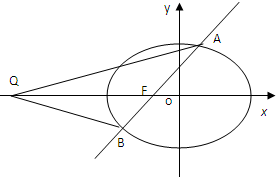已知椭圆C：