题目内容
14.已知双曲线方程为$\frac{{x}^{2}}{4}$-y2=1,双曲线上一点P(a,b)(b≠0)到直线y=x的距离是$\sqrt{2}$,求|a+b|的值.分析 由点到直线的距离得a-b=2或a-b=-2,把P(a,b)代入双曲线方程,求出a,b,即可求出|a+b|的值.
解答 解:∵双曲线$\frac{{x}^{2}}{4}$-y2=1上一点P(a,b)到直线y=x的距离为$\sqrt{2}$,
∴由点到直线的距离得a-b=2或a-b=-2,
把P(a,b)代入双曲线方程,得$\frac{{a}^{2}}{4}$-b2=1,
(a+2b)(a-2b)=4,
当a-b=2时,上式化为:(3b+2)(2-b)=4,b≠0解得b=$\frac{4}{3}$,|a+b|=|2b+2|=$\frac{11}{3}$.
当a-b=-2时,上式化为:(3b-2)(-2-b)=4,解得b=$±2\sqrt{2}$.
|a+b|=|2b-2|=4$\sqrt{2}±2$.
点评 本题考查双曲线的简单性质的应用,是中档题,解题时要注意点到直线的距离公式的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4.已知-9,a1,a2,-1成等差数列,-9,b1,b2,b3,-1成等比数列,则b2(a1+a2)等于( )
| A. | 30 | B. | -30 | C. | ±30 | D. | 15 |
2.已知几何体的三视图(如图),则该几何体的表面积为( )
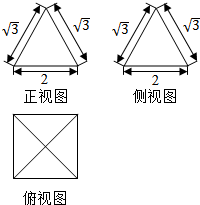

| A. | $4\sqrt{2}$ | B. | $4\sqrt{3}$ | C. | 4$\sqrt{2}$+4 | D. | 4$\sqrt{3}$+4 |
19.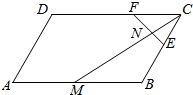 如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
 如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )| A. | $\frac{15}{14}$ | B. | 1 | C. | $\frac{5}{14}$ | D. | -$\frac{5}{14}$ |
6.在平面直角坐标系中,过点(0,1)且倾斜角为45°的直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知焦点在y轴上的双曲线$\frac{{x}^{2}}{m}$+y2=1,其准线方程为y=±$\frac{\sqrt{5}}{5}$,则实数m的值是( )
| A. | -4 | B. | -$\frac{1}{4}$ | C. | -4或-$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
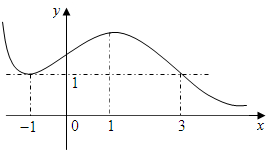 f′(x)为定义在R上的函数f(x)的导函数,而y=3f'(x)的图象如图所示,则y=f(x)的单调递增区间是(-∞,3].
f′(x)为定义在R上的函数f(x)的导函数,而y=3f'(x)的图象如图所示,则y=f(x)的单调递增区间是(-∞,3].