题目内容
5．如果关于x的不等式|x-2|+|x+3|≥a的解集为R，求参数a的取值范围．分析 问题等价为：对任意的实数x不等式|x-2|+|x+3|≥a恒成立，根据绝对值三角不等式求出[|x-2|+|x+3|]min=5即可．
解答 解：因为关于x的不等式|x-2|+|x+3|≥a的解集为R，
所以，对任意的实数x不等式|x-2|+|x+3|≥a恒成立，
即[|x-2|+|x+3|]min≥a，
根据绝对值三角不等式得，|x-2|+|x+3|≥|（x-2）-（x+3）|=5，
即[|x-2|+|x+3|]min=5，所以，a≤5，
因此，实数a的取值范围为：（-∞，5]．
点评 本题主要考查了绝对值不等式的解法，以及绝对值三角不等式的应用，属于中档题．
练习册系列答案
相关题目
16．双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$的渐近线与圆（x-3）2+y2=r2（r＞0）相切，则r=（ ）
| A． | $\frac{{6\sqrt{13}}}{13}$ | B． | $\frac{{6\sqrt{7}}}{7}$ | C． | $\frac{{6\sqrt{11}}}{11}$ | D． | $\sqrt{3}$ |
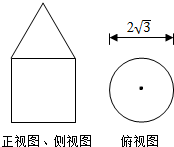如图，一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形，俯视图是一个半径为$\sqrt{3}$的圆（包括圆心）．则该组合体的表面积（各个面的面积的和）等于21π．