题目内容
4．已知-9，a1，a2，-1成等差数列，-9，b1，b2，b3，-1成等比数列，则b2（a1+a2）等于（ ）| A． | 30 | B． | -30 | C． | ±30 | D． | 15 |
分析 利用已知条件根据等差数列以及等比数列列出关系式求解即可．
解答 解：根据题意，由于-9，a1，a2，-1成等差数列，故等差中项的性质可知，
有a1+a2=-9-1=-10-9，b1，b2，b3，-1成等比数列，
则由等比中项性质得到，${b_2}^2={b_1}{b_3}=（-1）×（-9）=9$
由于奇数项的符号爱等比数列中相同，故b2=-3，因此b2（a1+a2）=30，
故选A．
点评 对于等差数列和等比数列的等差中项性质与等比性质的运用是数列考试题中常考的知识点，要熟练的掌握，同时能利用整体的思想来处理数列问题，也是很重要的一种思想，属于基础题．
练习册系列答案
相关题目
9．α是第四象限角，P（$\sqrt{5}$，x）为其终边上一点，且sinα=$\frac{\sqrt{2}}{4}$x，则cosα的值为（ ）
| A． | $\frac{\sqrt{10}}{4}$ | B． | $\frac{\sqrt{6}}{4}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | -$\frac{\sqrt{10}}{4}$ |
16．双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$的渐近线与圆（x-3）2+y2=r2（r＞0）相切，则r=（ ）
| A． | $\frac{{6\sqrt{13}}}{13}$ | B． | $\frac{{6\sqrt{7}}}{7}$ | C． | $\frac{{6\sqrt{11}}}{11}$ | D． | $\sqrt{3}$ |
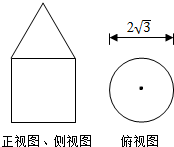如图，一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形，俯视图是一个半径为$\sqrt{3}$的圆（包括圆心）．则该组合体的表面积（各个面的面积的和）等于21π．