题目内容
已知函数f(x)=sin2x+
sinxcosx.
(Ⅰ)求f(
)的值;
(Ⅱ)当x∈[0,
]时,求函数f(x)的最大值和最小值.
| 3 |
(Ⅰ)求f(
| π |
| 12 |
(Ⅱ)当x∈[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(Ⅰ)借助于二倍角公式化简函数解析式:f(x)=sin(2x-
)+
,然后,求解f(
)的值;
(Ⅱ)首先,根据x∈[0,
],同时结合正弦函数的最值进行求解.
| π |
| 6 |
| 1 |
| 2 |
| π |
| 12 |
(Ⅱ)首先,根据x∈[0,
| π |
| 2 |
解答:
解:(Ⅰ)f(x)=sin2x+
sinxcosx
=
+
sin2x
=
sin2x-
cos2x+
=sin(2x-
)+
.
∴f(x)=sin(2x-
)+
.
所以f(
)=1.
(Ⅱ)当x∈[0,
]时,
-
≤2x-
≤
.
∴当2x-
=-
时,即x=0时,函数f(x)取得最小值0;
当2x-
=
时,即x=
时,函数f(x)取得最大值
.
| 3 |
=
| 1-cos2x |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
∴f(x)=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
所以f(
| π |
| 6 |
(Ⅱ)当x∈[0,
| π |
| 2 |
-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴当2x-
| π |
| 6 |
| π |
| 6 |
当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
点评:本题综合考查了二倍角公式、辅助角公式、三角函数的图象与性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知角α的终边经过点P(m,4),且cosα=-
,则m等于( )
| 3 |
| 5 |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
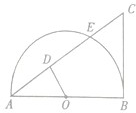 如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D.
如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D.