题目内容
为振兴旅游业，广西某旅游局2013年面向国内发行总量为100万张的优惠卡，向省外人士发行的是优惠金卡（简称金卡），向省内人士发行的是优惠银卡（简称银卡）．某旅游公司组织了一个有36名游客的旅游团到桂林名胜旅游，其中
是省外游客，其余是省内游客，在省外游客中有
持金卡，在省内游客中有
持银卡．
（1）在该团的省外游客中随机采访4名游客，求接受采访的4名游客中至少有2人持金卡的概率；
（2）在该团中随机采访4名游客，求恰有1人持金卡且持银卡者不多于2人的概率．
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
（1）在该团的省外游客中随机采访4名游客，求接受采访的4名游客中至少有2人持金卡的概率；
（2）在该团中随机采访4名游客，求恰有1人持金卡且持银卡者不多于2人的概率．
考点：互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：（1）由题意得，境外游客有27人，其中9人持金卡；境内游客有9人，其中6人持银卡．记出事件，表示出事件的概率，根据互斥事件的概率公式，得到结论．
（2）在该团的境内游客中随机采访4名游客，恰有1人持金卡且持银卡者不多于2人有三类分别求出其概率，再求其和，即可．
（2）在该团的境内游客中随机采访4名游客，恰有1人持金卡且持银卡者不多于2人有三类分别求出其概率，再求其和，即可．
解答：
解：由题意得，省外游客有27人，其中9人持金卡，省内游客有9人，其中6人持银卡
设至少有2人持金卡的概率为P，则P=1-
-
=
．
（2）设事件B为“采访该团3人中，恰有1人持金卡且持银卡者少于2人”，
事件A1为“采访该团4人中，1人持金卡，0人持银卡”，
事件A2为“采访该团4人中，1人持金卡，1人持银卡”，
事件A3为“采访该团4人中，1人持金卡，2人持银卡”．
P（B）=P（A1）+P（A2）+P（A3）=
+
+
=
+
+
=
所以，在该团中随机采访3人，恰有1人持金卡且持银卡者少于2人的概率是
．
设至少有2人持金卡的概率为P，则P=1-
| ||||
|
| ||
|
| 397 |
| 975 |
（2）设事件B为“采访该团3人中，恰有1人持金卡且持银卡者少于2人”，
事件A1为“采访该团4人中，1人持金卡，0人持银卡”，
事件A2为“采访该团4人中，1人持金卡，1人持银卡”，
事件A3为“采访该团4人中，1人持金卡，2人持银卡”．
P（B）=P（A1）+P（A2）+P（A3）=
| ||||
|
| ||||||
|
| ||||||
|
| 38 |
| 187 |
| 36 |
| 187 |
| 9 |
| 187 |
| 83 |
| 187 |
所以，在该团中随机采访3人，恰有1人持金卡且持银卡者少于2人的概率是
| 83 |
| 187 |
点评：本题考查运用概率知识解决实际问题的能力，注意满足独立重复试验的条件，解题过程中判断概率的类型是难点也是重点．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
函数f（x）=sin（ωx-
）（0＜ω＜4）图象的一条对称轴方程是x=
，将函数f（x）的图象沿x轴向左平移
得到函数g（x）的图象，则函数g（x）的解析式是（ ）
| π |
| 3 |
| 5π |
| 12 |
| π |
| 6 |
| A、g（x）=sin2x | ||||
B、g（x）=sin（2x-
| ||||
C、g（x）=sin（
| ||||
D、g（x）=sin（
|
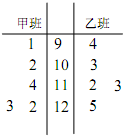为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取5名学生的成绩作样本，如图是样本的茎叶图．规定：成绩不低于120分时为优秀成绩．