题目内容
已知函数f(x)=ax+xlnx.
(1)当a=1时,函数f(x)的图象在点P(1,f(1))处的切线方程;
(2)当a<0时,解不等式f(x)<0;
(3)当a=1时,对x∈(1,+∞),直线y=k(x-1)恒在函数y=f(x)的图象下方.求整数k的最大值.
(1)当a=1时,函数f(x)的图象在点P(1,f(1))处的切线方程;
(2)当a<0时,解不等式f(x)<0;
(3)当a=1时,对x∈(1,+∞),直线y=k(x-1)恒在函数y=f(x)的图象下方.求整数k的最大值.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)求函数的导数,利用导数的几何意义求函数y=f(x)的图象在点P(1,f(1))处的切线l的方程;
(2)解对数不等式求得即可;
(3)由题意得问题等价于k<
=
对任意x>1恒成立,令g(x)=
,利用导数求得函数的最小值即可得出结论.
(2)解对数不等式求得即可;
(3)由题意得问题等价于k<
| f(x) |
| x-1 |
| x+xlnx |
| x-1 |
| x+xlnx |
| x-1 |
解答:
解:(1),当a=1时.f(x)=x+xlnx.∴f′(x)=2+lnx,
∴f′(1)=2,f(1)=1,
∴切线方程为y-1=2(x-1),即y=2x-1…(2分)
(2)∵f(x)=ax+xlnx,又函数的定义域为(0,+∞),
∴f(x)<0?a+lnx<0,∴x∈(0,e-a)…(4分)
(3)由a=1时,对x∈(1,+∞)时,直线y=k(x-1)恒在函数y=f(x)的图象下方得,
问题等价于k<
=
对任意x>1恒成立.…(5分)
令g(x)=
,∴g′(x)=
,
令h(x)=x-2-lnx,故h(x)在(1,+∞)上是增函数,
由于h(3)=1-ln3<0,h(4)=2-ln4>0
所以存在x0∈(3,4),使得h(x0)=x0-2-lnx0=0.
则x∈(1,x0)时,h(x)<0;x∈(x0,+∞)时,h(x)>0,
即x∈(1,x0)时,g'(x)<0;x∈(x0,+∞)时,g'(x)>0
知g(x)在(1,x0)递减,(x0,+∞)递增…(10分)
又g(x0)<g(3)=
(ln3+1)<g(4)=2+2ln4,所以kmax=3. …(12分)
∴f′(1)=2,f(1)=1,
∴切线方程为y-1=2(x-1),即y=2x-1…(2分)
(2)∵f(x)=ax+xlnx,又函数的定义域为(0,+∞),
∴f(x)<0?a+lnx<0,∴x∈(0,e-a)…(4分)
(3)由a=1时,对x∈(1,+∞)时,直线y=k(x-1)恒在函数y=f(x)的图象下方得,
问题等价于k<
| f(x) |
| x-1 |
| x+xlnx |
| x-1 |
令g(x)=
| x+xlnx |
| x-1 |
| x-2-lnx |
| (x-1)2 |
令h(x)=x-2-lnx,故h(x)在(1,+∞)上是增函数,
由于h(3)=1-ln3<0,h(4)=2-ln4>0
所以存在x0∈(3,4),使得h(x0)=x0-2-lnx0=0.
则x∈(1,x0)时,h(x)<0;x∈(x0,+∞)时,h(x)>0,
即x∈(1,x0)时,g'(x)<0;x∈(x0,+∞)时,g'(x)>0
知g(x)在(1,x0)递减,(x0,+∞)递增…(10分)
又g(x0)<g(3)=
| 3 |
| 2 |
点评:本题主要考查利用导数研究函数切线方程、单调性、最值等性质,考查学生的运算能力,综合性较强,难度较大.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知a=0,7-
,b=0.6-
,c=log2.11.5,则a,b,c的大小关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、c<a<b |
| B、c<b<a |
| C、a<b<c |
| D、b<a<c |
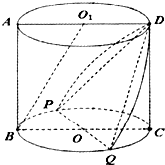 在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.
在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.