题目内容
设函数f(x)=(1+x)2-2ln(1+x)+2.
(1)求函数f(x)的单调区间;
(2)若对任意的a∈(1,2),总存在x0∈[1,2],使不等式f(x0)>a+
+m成立,求实数m的取值范围.
(1)求函数f(x)的单调区间;
(2)若对任意的a∈(1,2),总存在x0∈[1,2],使不等式f(x0)>a+
| 9 |
| 4a |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)利用导数法即可求得函数的单调区间;
(2)构造函数g(a)=a+
+m,由题意得,即证f(x)max>g(a)max,利用导数分别求出两函数的最大值,解不等式即得结论.
(2)构造函数g(a)=a+
| 9 |
| 4a |
解答:
解:(1)函数的定义域为(-1,+∞),
f′(x)=2[(x+1)-
]=
,
由f'(x)>0,得x>0;
由f'(x)<0,得-1<x<0
所以f(x)的递增区间是(0,+∞);递减区间是(-1,0).
(2)设g(a)=a+
+m,g′(a)=1-
=0,∴a=
∴y=g(a)在a∈(1,
)上单调递减,在a∈(
,2)上单调递增,
又由(1)知f(x)在[1,2]上单调递增,
∴f(x)max=f(2)=11-ln9…(12分)
又g(1)=
+m,g(2)=
+m,
∴g(1)>g(2),
∴若对任意的a∈(1,2),总存在x0∈[1,2],使不等式f(x0)>a+
+m成立,则
∴11-ln9>
+m
∴m<
-ln9.
f′(x)=2[(x+1)-
| 1 |
| x+1 |
| 2x(x+2) |
| x+1 |
由f'(x)>0,得x>0;
由f'(x)<0,得-1<x<0
所以f(x)的递增区间是(0,+∞);递减区间是(-1,0).
(2)设g(a)=a+
| 9 |
| 4a |
| 9 |
| 4a2 |
| 3 |
| 2 |
∴y=g(a)在a∈(1,
| 3 |
| 2 |
| 3 |
| 2 |
又由(1)知f(x)在[1,2]上单调递增,
∴f(x)max=f(2)=11-ln9…(12分)
又g(1)=
| 13 |
| 4 |
| 25 |
| 8 |
∴g(1)>g(2),
∴若对任意的a∈(1,2),总存在x0∈[1,2],使不等式f(x0)>a+
| 9 |
| 4a |
∴11-ln9>
| 13 |
| 4 |
∴m<
| 31 |
| 4 |
点评:本题考查利用导数判断函数的单调性及求函数的最大值等知识,考查等价转化思想的运用能力,属难题.

练习册系列答案
相关题目
已知函数f(x)=
x2+(a-1)x+3在区间(-∞,4]上单调递减,则a的取值范围( )
| 1 |
| 2 |
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-∞,-3) |
| D、(-∞,-3] |
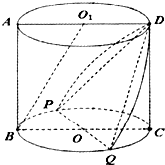 在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.
在如图所示的圆柱OO1中,过轴OO1作截面ABCD.已知PQ是圆O异于BC的直径.