Question

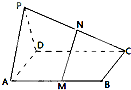如图，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB，PC的中点
（1）求证：MN∥平面PAD；
（2）若△PAD为正三角形，求异面直线PA与MN所成的角的大小．

Answer 1

考点：异面直线及其所成的角,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）根据直线和平面平行的判定定理即可得到结论．
（2）根据异面直线所成角的定义即可得到结论．

解答： 解：（1）取PD的中点H，连结AH，
∵N是PC的中点，∴NH∥DC，NH=

1

2

DC，
∵M是AB的中点，∴NH∥AM，且NH=AM，
即AMNH为平行四边形，∴MN∥AH，
∵AN?平面PAD，AH?平面PAD，
∴MN∥平面PAD
（2）由（1）知MN∥AH，
则∠PAH就是异面直线PA与MN所成的角，
∵△PAD为正三角形，
∴∠PAH=30°，
即异面直线PA与MN所成的角的大小为30°．

点评：本题主要考查异面直线所成角的求解以及直线和平面平行的判断，要求熟练掌握线面平行的判定定理．