题目内容
已知正四棱锥P-ABCD的棱长都相等，侧棱PB、PD的中点分别为M、N，则截面AMN与底面ABCD所成的二面角的余弦值是 ．
考点：二面角的平面角及求法
专题：计算题,空间位置关系与距离
分析：正四棱锥P-ABCD中，O为正方形ABCD的两对角线的交点，则PO⊥面ABCD，PO交MN于E，过A作直线l∥BD，则l⊥EA，l⊥AO，可得∠EAO为所求二面角的平面角，即可得出结论．
解答：
解：
如图，正四棱锥P-ABCD中，O为正方形ABCD的两对角线的交点，则PO⊥面ABCD，PO交MN于E，则PE=EO，
又BD⊥AC，∴BD⊥面PAC，
过A作直线l∥BD，则l⊥EA，l⊥AO，
∴∠EAO为所求二面角的平面角．
又EO=
AO=
a，AO=
a，∴AE=
a
∴cos∠EAO=
．
∴截面AMN与底面ABCD所成的二面角的余弦值是
．
如图，正四棱锥P-ABCD中，O为正方形ABCD的两对角线的交点，则PO⊥面ABCD，PO交MN于E，则PE=EO，又BD⊥AC，∴BD⊥面PAC，
过A作直线l∥BD，则l⊥EA，l⊥AO，
∴∠EAO为所求二面角的平面角．
又EO=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
∴cos∠EAO=
2
| ||
| 5 |
∴截面AMN与底面ABCD所成的二面角的余弦值是
2
| ||
| 5 |
点评：本题考查截面AMN与底面ABCD所成的二面角的余弦值，考查学生的计算能力，正确作出二面角的平面角是关键．
练习册系列答案
字词句段篇系列答案
相关题目
设集合U=R，M={x|x＞2011}，N={x|0＜x＜1}，则下列关系中正确的是（ ）
| A、M∪（∁UN）=R |
| B、M∩N={x|0＜x＜1} |
| C、N⊆∁UM |
| D、M∩N≠∅ |
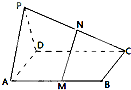如图，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB，PC的中点
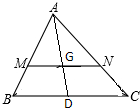如图，△ABC中，D为BC的中点，G为AD的中点，过点G任作一直线MN，分别交AB，AC于M，N两点，若