题目内容
2014年秋,某校决定派遣语、数、外、物、化、生六科的骨干教师各一人去甲乙两所学校支教,每校至少一人,且物理教师和化学教师必须分在同一所学校.
(Ⅰ)求语文教师和数学教师分在不同学校的概率;
(Ⅱ)用X、Y分别表示这6个人中去甲、乙两校支教的人数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望Eξ.
(Ⅰ)求语文教师和数学教师分在不同学校的概率;
(Ⅱ)用X、Y分别表示这6个人中去甲、乙两校支教的人数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望Eξ.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)利用捆绑法分类求出把6名教师分到两所学校的所有不同分法,然后把除了语文和数学教师外的4名教师分给语文和数学教师(4人可分给同一名教师),再排列到两所学校,求出语文教师和数学教师分在不同学校的方法种数,由古典概型概率计算公式求得语文教师和数学教师分在不同学校的概率;
(Ⅱ)根据X、Y的不同取值情况求出ξ=|X-Y|的值,再由古典概型概率计算公式求得概率,列出分布列,代入期望公式求期望.
(Ⅱ)根据X、Y的不同取值情况求出ξ=|X-Y|的值,再由古典概型概率计算公式求得概率,列出分布列,代入期望公式求期望.
解答:
解:把物理教师和化学教师捆绑,看作1人,问题是把5人分到两所不同的学校,每校至少1人,
共有不同的分法种数为:
•
+
•
+
•
+
•
=30.
(Ⅰ)语文教师和数学教师分在不同学校,所有不同的分法种数为:(
+
+
+
)•
=16.
则语文教师和数学教师分在不同学校的概率为P=
=
;
(Ⅱ)X、Y的取值分别为:
X:1 2 3 4 5
Y:5 4 3 2 1.
ξ=|X-Y|=0或2或4.
当P(ξ=0)=
=
.
当P(ξ=2)=2×
=
.
当P(ξ=4)=
=
.
随机变量ξ的分布列如图:
∴E(ξ)=0×
+2×
+4×
=2.
共有不同的分法种数为:
| C | 1 5 |
| C | 4 4 |
| C | 2 5 |
| C | 3 3 |
| C | 3 5 |
| C | 2 2 |
| C | 4 5 |
| C | 1 1 |
(Ⅰ)语文教师和数学教师分在不同学校,所有不同的分法种数为:(
| C | 0 3 |
| C | 1 3 |
| C | 2 3 |
| C | 3 3 |
| A | 2 2 |
则语文教师和数学教师分在不同学校的概率为P=
| 16 |
| 30 |
| 8 |
| 15 |
(Ⅱ)X、Y的取值分别为:
X:1 2 3 4 5
Y:5 4 3 2 1.
ξ=|X-Y|=0或2或4.
当P(ξ=0)=
| ||||
| 30 |
| 4 |
| 15 |
当P(ξ=2)=2×
1+
| ||
| 30 |
| 7 |
| 15 |
当P(ξ=4)=
| ||||
| 30 |
| 4 |
| 15 |
随机变量ξ的分布列如图:
| ξ | 0 | 2 | 4 | ||||||
| P |
|
|
|
| 4 |
| 15 |
| 7 |
| 15 |
| 4 |
| 15 |
点评:不同考查了古典概型及其概率计算公式,考查了离散型随机变量的分布列及数学期望的求法,关键是概率的计算,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a,b均为非零实数,集合A={x|x=
+
},则集合A的元素的个数为( )
| |a| |
| a |
| b |
| |b| |
| A、1 | B、2 | C、3 | D、4 |
圆锥的侧面展开图是直径为4a的半圆面,那么此圆锥的轴截面是( )
| A、等边三角形 |
| B、等腰直角三角形 |
| C、顶角为30°的等腰三角形 |
| D、其他等腰三角形 |
设集合U=R,M={x|x>2011},N={x|0<x<1},则下列关系中正确的是( )
| A、M∪(∁UN)=R |
| B、M∩N={x|0<x<1} |
| C、N⊆∁UM |
| D、M∩N≠∅ |
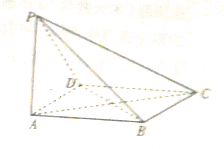 如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.
如图,四边形ABCD是菱形,PA⊥ABCD,AD=2,∠BAD=60°.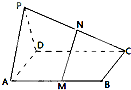 如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB,PC的中点
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB,PC的中点