题目内容
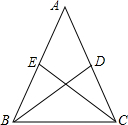 如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.
如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.考点:解三角形
专题:综合题,推理和证明
分析:连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,DE为△ABC的中位线,故BC=4x,四边形BCDE为等腰梯形,根据等腰梯形的性质可知,BF=
(BC-DE)=x,则FC=3x,又△BCG为等腰直角三角形,故△CEF为等腰直角三角形,则EF=CF=3x,解Rt△BEF可求解cos∠BEF,利用二倍角公式可得顶角∠A的余弦值.
| 1 |
| 2 |
解答:
 解:如图,连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,
解:如图,连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,
依题意,得DE为△ABC的中位线,∴BC=4x,
又∵四边形BCDE为等腰梯形,
∴BF=
(BC-DE)=x,则FC=3x,
∵BD⊥CE,
∴△BCG为等腰直角三角形,
∵EF⊥BC,
∴△CEF为等腰直角三角形,
∴EF=CF=3x,
在Rt△BEF中,EF=3x,BF=x,BE=
x
∴cos∠BEF=
,
∴cos∠A=2cos2∠BEF-1=2×
-1=
.
 解:如图,连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,
解:如图,连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,依题意,得DE为△ABC的中位线,∴BC=4x,
又∵四边形BCDE为等腰梯形,
∴BF=
| 1 |
| 2 |
∵BD⊥CE,
∴△BCG为等腰直角三角形,
∵EF⊥BC,
∴△CEF为等腰直角三角形,
∴EF=CF=3x,
在Rt△BEF中,EF=3x,BF=x,BE=
| 10 |
∴cos∠BEF=
| 3 | ||
|
∴cos∠A=2cos2∠BEF-1=2×
| 9 |
| 10 |
| 4 |
| 5 |
点评:本题考查了锐角三角函数值的求法,三角形中位线定理,梯形的性质.求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法,把问题转化到直角三角形中求三角函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}是等差数列,若a2+2,a4+4,a6+6构成等比数列,这数列{an}的公差d等于( )
| A、1 | B、-1 | C、2 | D、-2 |
已知圆O:x2+y2=1和直线l:y=kx+
,则k=1是圆O与直线l相切的( )
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |