题目内容
已知圆O：x2+y2=1和直线l：y=kx+
，则k=1是圆O与直线l相切的（ ）
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断,直线与圆的位置关系
专题：计算题,直线与圆,简易逻辑
分析：圆O与直线l相切，可得圆心到直线的距离d=
=1，求出k，即可得出结论．
| ||
|
解答：
解：∵圆O与直线l相切，
∴圆心到直线的距离d=
=1，
∴k=±1，
∴k=1是圆O与直线l相切的充分不必要条件．
故选：B．
∴圆心到直线的距离d=
| ||
|
∴k=±1，
∴k=1是圆O与直线l相切的充分不必要条件．
故选：B．
点评：本题考查直线与圆的位置关系，考查学生的计算能力，考查充要条件的判断，正确运用点到直线的距离公式是关键．
练习册系列答案
相关题目
若等边△ABC的边长为2
，平面内一点M满足：
=
+
，则
•
=（ ）
| 3 |
| CM |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| MA |
| MB |
| A、-1 | B、2 | C、-2 | D、3 |
定义域为R的函数f（x）满足f（x+2）=2f（x）-2，当x∈（0，2]时，f（x）=
，若x∈（0，4]时，t2-
≤f（x）恒成立，则实数t的取值范围是（ ）
|
| 7t |
| 2 |
| A、[1，2] | ||
B、[2，
| ||
C、[1，
| ||
| D、[2，+∞） |
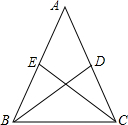如图，在等腰△ABC中，两腰上的中线分别为BD、CE，且BD⊥CE，求顶角∠A的余弦值．
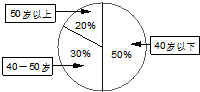某单位200名职工的年龄分布情况如图示，该单位为了解职工每天的睡眠情况，按年龄用分层抽样方法从中抽取40名职工进行调查．则应从40-50岁的职工中抽取的人数为（ ）