题目内容
已知函数f(x)=4sinωx•cos(ωx+
)+
,(ω>0)的最小正周期是π,求函数f(x)在[-
,
]上的单调区间.
| π |
| 3 |
| 3 |
| π |
| 4 |
| π |
| 6 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:首先利用三角函数关系式的恒等变换求出函数的解析式为正弦型函数,进一步利用函数的周期求出函数的解析式,再利用整体思想在定义域内求出函数的单调区间.
解答:
解:f(x)=4sinωx•cos(ωx+
)+
=4sinωx(
cosωx-
sinωx)+
=sin2ωx-
cos2ωx
=2sin(2ωx-
),
由于函数f(x)的最小正周期是π.
所以:T=
=π,
解得:ω=1,
所以函数的解析式为:f(x)=2sin(2x-
).
令:-
+2kπ≤2x-
≤
+2kπ,
解得:-
+kπ≤x≤
+kπ,
所以:函数的单调递增区间为:[-
,
].
函数的单调递减区间为:[-
,-
].
| π |
| 3 |
| 3 |
=4sinωx(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=sin2ωx-
| 3 |
=2sin(2ωx-
| π |
| 3 |
由于函数f(x)的最小正周期是π.
所以:T=
| 2π |
| 2ω |
解得:ω=1,
所以函数的解析式为:f(x)=2sin(2x-
| π |
| 3 |
令:-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得:-
| π |
| 12 |
| 5π |
| 12 |
所以:函数的单调递增区间为:[-
| π |
| 12 |
| π |
| 6 |
函数的单调递减区间为:[-
| π |
| 4 |
| π |
| 12 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,利用函数的周期求函数的解析式,利用整体思想求正弦型函数的单调区间.

练习册系列答案
相关题目
曲线y=
(a≠0)与y=2x+1在x=b处相切,则a+b=( )
| x |
| x+a |
| A、1 | B、-1 | C、2 | D、-2 |
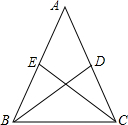 如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.
如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.