题目内容
已知关于x的不等式|2x-1|-|x-1|≤log2a.
(1)当a=8时,求不等式解集.
(2)若不等式有解,求a的范围.
(1)当a=8时,求不等式解集.
(2)若不等式有解,求a的范围.
考点:绝对值不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)当a=8时,化简不等式通过去绝对值符号,求解不等式得到解集.
(2)若不等式有解,转化为函数的最值问题,然后求a的范围.
(2)若不等式有解,转化为函数的最值问题,然后求a的范围.
解答:
解:(1)由题意可得:|2x-1|-|x-1|≤3…(1分)
当x≤
时,-2x+1+x-1≤3,x≥-3,即-3≤x≤
…(2分)
当
<x<1时,2x-1+x-1≤3,即x≤
…(3分)
当x≥1时,2x-1-x+1≤3,即x≤3…(4分)
∴该不等式解集为{x|-3≤x≤3}.…(5分)
(2)令f(x)=|2x-1|-|x-1|,有题意可知:lo
≥f(x)min…(6分)
又∵f(x)=
…(8分)
∴f(x)min=-
…(9分)
即a≥2-
=
,…(10分)
当x≤
| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |
| 5 |
| 3 |
当x≥1时,2x-1-x+1≤3,即x≤3…(4分)
∴该不等式解集为{x|-3≤x≤3}.…(5分)
(2)令f(x)=|2x-1|-|x-1|,有题意可知:lo
| g | a 2 |
又∵f(x)=
|
∴f(x)min=-
| 1 |
| 2 |
即a≥2-
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查绝对值不等式的解法,函数的最值以及几何意义,考查分类讨论思想以及计算能力.

练习册系列答案
相关题目
已知数列{an}中,a1=1,an+1=2an+3n,则下列结论错误的是( )
A、{
| ||
| B、{an-3n}成等比数列 | ||
| C、{an+2n}成等比数列 | ||
| D、{an-2n}成等比数列 |
已知函数f(x)满足f(x)=f(
)且当x∈[
,1]时,f(x)=lnx,若当x∈[
,π]时,函数g(x)=f(x)-ax与x轴有交点,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| π |
| 1 |
| π |
A、[-
| ||||
| B、[-πlnπ,0] | ||||
C、[-
| ||||
D、[-
|
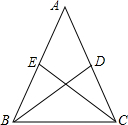 如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.
如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.
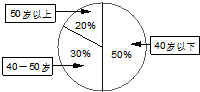 某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )
某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( ) 某中学从甲、乙两个艺术班中各选出7名学生参加市级才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名学生参加市级才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为( )