题目内容
在△ABC中,记角A、B、C所对的边长分别为a、b、c,若
•
<0,则下列结论中:
①△ABC是钝角三角形; ②a2>b2+c2;
③cosBcosC>sinBsinC; ④sinB>cosC;
其中错误结论的序号是 .
| AB |
| AC |
①△ABC是钝角三角形; ②a2>b2+c2;
③cosBcosC>sinBsinC; ④sinB>cosC;
其中错误结论的序号是
考点:余弦定理,平面向量数量积的运算
专题:解三角形
分析:由条件可得∠A 为钝角,故①、②正确;再根据cosA<0,可得③正确;根据B+C<
,正弦函数的单调性、诱导公式可得④不正确,从而得出结论.
| π |
| 2 |
解答:
解:△ABC中,∵
•
<0,则∠A 为钝角,故①、②正确.
再根据cosA=-cos(B+C)=-cosBcosC+sinBsinC<0,化简可得cosBcosC>sinBsinC,故③正确.
根据B+C<
,可得0<B<
-C<
,∴sinB<sin(
-C)=cosC,即 sinB<cosC,故④错误,
故答案为:④.
| AB |
| AC |
再根据cosA=-cos(B+C)=-cosBcosC+sinBsinC<0,化简可得cosBcosC>sinBsinC,故③正确.
根据B+C<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为:④.
点评:本题主要考查两个向量的数量积的定义,诱导公式、两角和的余弦公式,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
已知函数f(x)满足f(x)=f(
)且当x∈[
,1]时,f(x)=lnx,若当x∈[
,π]时,函数g(x)=f(x)-ax与x轴有交点,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| π |
| 1 |
| π |
A、[-
| ||||
| B、[-πlnπ,0] | ||||
C、[-
| ||||
D、[-
|
 某中学从甲、乙两个艺术班中各选出7名学生参加市级才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学从甲、乙两个艺术班中各选出7名学生参加市级才艺比赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为( )| A、6 | B、8 | C、9 | D、11 |
复数
-
(其中i为虚数单位)的虚部是( )
| 3-2i |
| 2+3i |
| 3+2i |
| 2-3i |
| A、-2 | B、-1 | C、1 | D、2 |
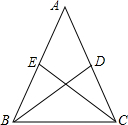 如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.
如图,在等腰△ABC中,两腰上的中线分别为BD、CE,且BD⊥CE,求顶角∠A的余弦值.