题目内容
设函数f（x）=
，若f（f（e））=1（e是自然对数的底数），则a的值为（ ）
|
| A、1 | B、2 | C、-1 | D、-2 |
考点：分段函数的应用
专题：函数的性质及应用
分析：直接利用分段函数以及定积分的运算法则求解a的值即可．
解答：
解：函数f（x）=
，
∴f（e）=1-lne=0．
而
3t2dt=t3
=a3．
∵f（f（e））=1，∴f（0）=1，
∴a3=1
解得a=1．
故选：A．
|
∴f（e）=1-lne=0．
而
| ∫ | a 0 |
| | | a 0 |
∵f（f（e））=1，∴f（0）=1，
∴a3=1
解得a=1．
故选：A．
点评：本题考查分段函数的应用，定积分的求法，函数的零点与方程的根的关系，考查计算能力．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
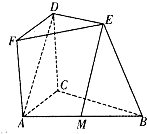如图，四边形ACDF为正方形，且平面ACDF⊥平面BCDE，平面ACDF⊥平面ABC，BC=2DE，DE∥BC，M为AB的中点．
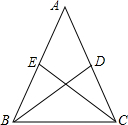如图，在等腰△ABC中，两腰上的中线分别为BD、CE，且BD⊥CE，求顶角∠A的余弦值．
已知数列{an}中，a1=1，an+1=2an+3n，则下列结论错误的是（ ）
A、{
| ||
| B、{an-3n}成等比数列 | ||
| C、{an+2n}成等比数列 | ||
| D、{an-2n}成等比数列 |