题目内容
已知数列{an}满足a1=4,an+1an+6an+1-4an-8=0,记bn=
.
(1)求数列{bn}的通项公式;
(2)求数列{an•bn}的前n项和Sn.
| 6 |
| an-2 |
(1)求数列{bn}的通项公式;
(2)求数列{an•bn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题意可证得数列∴{bn+1}是首项是b1+1=
+1=4,公比为4的等比数列,即可得出结论;
(2)分组后利用等比数列求和即可.
| 6 |
| 4-2 |
(2)分组后利用等比数列求和即可.
解答:
解:(1)∵bn=
,
∴an=
+2,
又∵an+1an+6an+1-4an-8=0,
∴(
+2)(
+2)+6(
+2)-4(
+2)-8=0,
整理得bn+1=4bn+3
bn+1+1=4(bn+1)
∴{bn+1}是首项是b1+1=
+1=4,公比为4的等比数列,
∴bn+1=4×4n-1=4n,
∴bn=4n-1.
(2)anbn=(
+2)bn=2bn+6=2×4n+4=22n+1+4,
∴sn=(23+25+…+22n+1)+4n=
+4n=
.
| 6 |
| an-2 |
∴an=
| 6 |
| bn |
又∵an+1an+6an+1-4an-8=0,
∴(
| 6 |
| bn+1 |
| 6 |
| bn |
| 6 |
| bn+1 |
| 6 |
| bn |
整理得bn+1=4bn+3
bn+1+1=4(bn+1)
∴{bn+1}是首项是b1+1=
| 6 |
| 4-2 |
∴bn+1=4×4n-1=4n,
∴bn=4n-1.
(2)anbn=(
| 6 |
| bn |
∴sn=(23+25+…+22n+1)+4n=
| 23(1-4n) |
| 1-4 |
| 22n+3+12n-8 |
| 3 |
点评:本题主要考查等比数列的定义及等比数列的求和公式等知识,考查学生的运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列现象是不可能现象的是( )
| A、导电通电时发热 |
| B、不共线的三点确定一个平面 |
| C、没有水分种子发芽 |
| D、某人买彩票连续两周都中奖 |
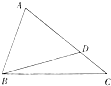 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC= 设
设