题目内容
已知向量
=（-x+1，2），
=（3，x），若
⊥
，则x等于（ ）
| a |
| b |
| a |
| b |
| A、-3 | B、-1 | C、1 | D、3 |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由题意可得
•
=3（-x+1）+2x=0，解方程可得．
| a |
| b |
解答：
解：∵向量
=（-x+1，2），
=（3，x），
由
⊥
可得
•
=3（-x+1）+2x=0，
解得x=3
故选：D
| a |
| b |
由
| a |
| b |
| a |
| b |
解得x=3
故选：D
点评：本题考查数量积与向量的垂直关系，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
△ABC的三边长分别为2m+3，m2+2m，m2+3m+3（m＞0），则最大内角的度数为（ ）
| A、150° | B、120° |
| C、90° | D、135° |
已知实数x、y满足ax＜ay（a＞1），则下列关系恒成立的是（ ）
| A、x3＜y3 | ||||
| B、tanx＜tany | ||||
| C、ln（x2+1）＜ln（y2+1） | ||||
D、
|
若{an}是等差数列，首项a1＞0，a2007+a2008＞0，a2007•a2008＜0，则使数列{an}的前n项和Sn为正数的最大自然数n是（ ）
| A、40013 | B、4014 |
| C、4015 | D、4016 |
下列说法正确的是（ ）
| A、“a＞b”是“a2＞b2”的必要条件 | ||
| B、“若a，b都是偶数，则a+b是偶数”的否命题为真 | ||
C、若x，y∈R，则“x=y”是“xy≤（
| ||
| D、已知命题p，q，若（￢p）∨q为假命题，则p∧（￢q）为真命题 |
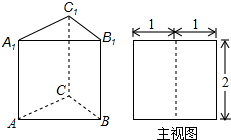如图，三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，且侧棱AA1⊥底面ABC，其主视图是边长为2的正方形，则此三棱柱左视图的面积为（ ）