题目内容
解下列各一元二次不等式:
(1)4x2≥0;
(2)x-x2+6<0;
(3)x2+x+3≥0;
(4)x2+x-6<0;
(5)2x2+3x-6<3x2+x-1;
(6)-x2-3x+10≥0.
(1)4x2≥0;
(2)x-x2+6<0;
(3)x2+x+3≥0;
(4)x2+x-6<0;
(5)2x2+3x-6<3x2+x-1;
(6)-x2-3x+10≥0.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:根据一元二次不等式的解法,结合不等式的特点,选择适当的解法,进行解答即可.
解答:
解:(1)∵4x2≥0,∴x2≥0,∴解得x∈R,∴不等式的解集为R;
(2)∵x-x2+6<0,∴x2-x-6>0,即(x+2)(x-3)>0,解得x<-2或x>3,
∴不等式的解集为(-∞,-2)∪(3,+∞);
(3)∵x2+x+3≥0,且△=12-4×1×3=-11<0,∴原不等式的解集为R;
(4)∵x2+x-6<0可化为(x+3)(x-2)<0,解得x<-3或x>2,
∴不等式的解集为(-∞,-3)∪(2,+∞);
(5)∵2x2+3x-6<3x2+x-1,∴x2-2x+5>0,且△=(-2)2-4×1×5=-16<0,
∴原不等式的解集为R;
(6)∵-x2-3x+10≥0,∴x2+3x-10≤0,即(x+5)(x-2)≤0,解得x≤-5或x≥2,
∴原不等式的解集为{x|x≤-5或x≥2}.
(2)∵x-x2+6<0,∴x2-x-6>0,即(x+2)(x-3)>0,解得x<-2或x>3,
∴不等式的解集为(-∞,-2)∪(3,+∞);
(3)∵x2+x+3≥0,且△=12-4×1×3=-11<0,∴原不等式的解集为R;
(4)∵x2+x-6<0可化为(x+3)(x-2)<0,解得x<-3或x>2,
∴不等式的解集为(-∞,-3)∪(2,+∞);
(5)∵2x2+3x-6<3x2+x-1,∴x2-2x+5>0,且△=(-2)2-4×1×5=-16<0,
∴原不等式的解集为R;
(6)∵-x2-3x+10≥0,∴x2+3x-10≤0,即(x+5)(x-2)≤0,解得x≤-5或x≥2,
∴原不等式的解集为{x|x≤-5或x≥2}.
点评:本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
过直线x=-
上一点P分别作圆C1:x2+y2=1和圆C2:(x-1)2+y2=9的切线,切点分别是M、N,则|PM|和|PN|的大小关系是:( )
| 7 |
| 2 |
| A、|PM|>|PN| |
| B、|PM|<|PN| |
| C、|PM|=|PN| |
| D、不能确定 |
已知向量
=(-x+1,2),
=(3,x),若
⊥
,则x等于( )
| a |
| b |
| a |
| b |
| A、-3 | B、-1 | C、1 | D、3 |
已知函数f(x)=2x+
,g(x)=log2(2+x)-log2(2-x),则( )
| 1 |
| 2x |
| A、f(x)与g(x)与均为奇函数 |
| B、f(x)为奇函数,g(x)为偶函数 |
| C、f(x)与g(x)与均为偶函数 |
| D、f(x)为偶函数,g(x)为奇函数 |
当a≠0时,函数y=ax+b和函数y=bax的图象可能是( )
A、 |
B、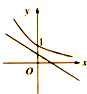 |
C、 |
D、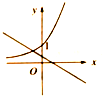 |
若a>0,a≠1,且m>0,n>0,则下列各式中正确的是( )
| A、logam•logan=loga(m+n) | ||||||||||
| B、am•an=am•n | ||||||||||
C、
| ||||||||||
| D、1÷an=a0-n |
y=2sin(
x-
)的周期为( )
| 1 |
| 2 |
| π |
| 6 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |