题目内容
下列说法正确的是( )
| A、“a>b”是“a2>b2”的必要条件 | ||
| B、“若a,b都是偶数,则a+b是偶数”的否命题为真 | ||
C、若x,y∈R,则“x=y”是“xy≤(
| ||
| D、已知命题p,q,若(¬p)∨q为假命题,则p∧(¬q)为真命题 |
考点:命题的真假判断与应用
专题:阅读型,不等式的解法及应用,简易逻辑
分析:举a=-2,b=-1,结合充分必要条件的定义,即可判断A;
求出逆命题,判断真假,再由互为逆否命题等价,即可判断B;
由充分必要条件的定义和基本不等式,即可判断C;
运用复合命题的真假和真值表,即可判断D.
求出逆命题,判断真假,再由互为逆否命题等价,即可判断B;
由充分必要条件的定义和基本不等式,即可判断C;
运用复合命题的真假和真值表,即可判断D.
解答:
解:对于A.“a>b”不能推出“a2>b2”,反之也不能推出,比如a=-2,b=-1,则A错;
对于B.“若a,b都是偶数,则a+b是偶数”的逆命题为“若a+b是偶数,则a,b都是偶数”,
显然错误,比如a,b可能都是奇数,则逆命题错,即有否命题也为错,则B错;
对于C.若x,y∈R,则“x=y”可得“xy≤(
)2”,反之若xy≤(
)2,
则化简可得(x-y)2≥0,则x=y不成立,则C错;
对于D.若(¬p)∨q为假命题,则q为假,p为真,¬q为真,即有p∧(¬q)为真命题,则D对.
故选D.
对于B.“若a,b都是偶数,则a+b是偶数”的逆命题为“若a+b是偶数,则a,b都是偶数”,
显然错误,比如a,b可能都是奇数,则逆命题错,即有否命题也为错,则B错;
对于C.若x,y∈R,则“x=y”可得“xy≤(
| x+y |
| 2 |
| x+y |
| 2 |
则化简可得(x-y)2≥0,则x=y不成立,则C错;
对于D.若(¬p)∨q为假命题,则q为假,p为真,¬q为真,即有p∧(¬q)为真命题,则D对.
故选D.
点评:本题考查简易逻辑的知识,考查充分必要条件的判断和复合命题的真假以及真值表的运用,考查基本不等式的运用,属于基础题和易错题.

练习册系列答案
相关题目
已知向量
=(-x+1,2),
=(3,x),若
⊥
,则x等于( )
| a |
| b |
| a |
| b |
| A、-3 | B、-1 | C、1 | D、3 |
已知函数f(x)=2x+
,g(x)=log2(2+x)-log2(2-x),则( )
| 1 |
| 2x |
| A、f(x)与g(x)与均为奇函数 |
| B、f(x)为奇函数,g(x)为偶函数 |
| C、f(x)与g(x)与均为偶函数 |
| D、f(x)为偶函数,g(x)为奇函数 |
当a≠0时,函数y=ax+b和函数y=bax的图象可能是( )
A、 |
B、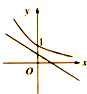 |
C、 |
D、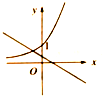 |
下列命题错误的是( )
| A、命题“若 lgx=0,则x=l”的逆否命题为“若x≠1,则lgx≠0” | ||||
| B、若 p∧q为假命题,则p,q均为假命题 | ||||
| C、命题 p:?x∈R,使得sinx>l,则¬p:?x∈R,均有 sinx≤1 | ||||
D、“x>2”是“
|
若a>0,a≠1,且m>0,n>0,则下列各式中正确的是( )
| A、logam•logan=loga(m+n) | ||||||||||
| B、am•an=am•n | ||||||||||
C、
| ||||||||||
| D、1÷an=a0-n |
 已知全集U={1,2,3,4},集合A={1,2,4},B={2,3},则图中阴影部分表示的集合为( )
已知全集U={1,2,3,4},集合A={1,2,4},B={2,3},则图中阴影部分表示的集合为( )| A、{2} |
| B、{3} |
| C、{1,4} |
| D、{1,2,3,4} |