题目内容
已知实数x、y满足ax<ay(a>1),则下列关系恒成立的是( )
| A、x3<y3 | ||||
| B、tanx<tany | ||||
| C、ln(x2+1)<ln(y2+1) | ||||
D、
|
考点:不等关系与不等式,指数函数的图像与性质
专题:函数的性质及应用,不等式的解法及应用
分析:实数x、y满足ax<ay(a>1),可得x<y.
A.利用y=x3在R上单调递增,即可判断出;
B.取x=-
π,y=
,即可判断出;
C.取x=-2,y=-1,即可判断出;
D.取x=0,y=1,即可判断出.
A.利用y=x3在R上单调递增,即可判断出;
B.取x=-
| 3 |
| 4 |
| π |
| 6 |
C.取x=-2,y=-1,即可判断出;
D.取x=0,y=1,即可判断出.
解答:
解:∵实数x、y满足ax<ay(a>1),
∴x<y.
对于A.利用y=x3在R上单调递增,可得x3<y3,正确;
对于B.取x=-
π,y=
,但是tanx=1,tany=
,tanx<tany不成立;
对于C.取x=-2,y=-1,ln(x2+1)<ln(y2+1)不成立;
对于D.取x=0,y=1,
<
,不成立.
故选:A.
∴x<y.
对于A.利用y=x3在R上单调递增,可得x3<y3,正确;
对于B.取x=-
| 3 |
| 4 |
| π |
| 6 |
| ||
| 3 |
对于C.取x=-2,y=-1,ln(x2+1)<ln(y2+1)不成立;
对于D.取x=0,y=1,
| 1 |
| x2+1 |
| 1 |
| y2+1 |
故选:A.
点评:本题考查了函数的单调性、不等式的性质,考查了推理能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下表表示y是x的函数,则函数的值域是( )
| x | 0<x<5 | 5≤x<10 | 10≤x<15 | 15≤x≤20 |
| y | 2 | 3 | 4 | 5 |
| A、[2,5] |
| B、N |
| C、(0,20] |
| D、{2,3,4,5} |
已知向量
=(-x+1,2),
=(3,x),若
⊥
,则x等于( )
| a |
| b |
| a |
| b |
| A、-3 | B、-1 | C、1 | D、3 |
当a≠0时,函数y=ax+b和函数y=bax的图象可能是( )
A、 |
B、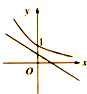 |
C、 |
D、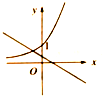 |