题目内容
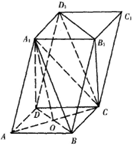 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,O是底面ABCD的对角线的交点,A1A=A1C,A1A⊥BC.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,O是底面ABCD的对角线的交点,A1A=A1C,A1A⊥BC.(1)证明:平面A1BC∥平面CD1B1;
(2)证明:A1O⊥平面ABC.
考点:直线与平面垂直的判定,平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)运用几何性质判断A1B∥B1C,A1D∥B1C.再运用定理判断.(2)运用性质判断出DB⊥平面A1AO,BD⊥A1O,A1O⊥AC,再运用判定定理证明.
解答:
证明:(1)易知AA1∥DD1,

∵底面ABCD为菱形,∴AB∥CD,
又∵AA1∩AB=A,CD∩DD1=D,
∴平面AA1BB1∥平面DC1CD1,
又A1B?平面AA1BB1,CD1?平面DC1CD1,
平面A1BCD1∩平面AA1BB1=A1B,
平面ABCBD1∩平面DC1CD1=D1C,
∴A1B∥B1C,
同理可证:A1D∥B1C.
又∵A1D∩A1B=A1,D1C∩B1C=C,
∴平面A1BC∥平面CD1B1;
(2)∵底面ABCD为菱形,∴AC⊥BD,
又∵AA1⊥BD,AA1∩AC=A,∴DB⊥平面A1AO,
∵A1O?平面A1AO,∴BD⊥A1O,
由∵A1A=A1C,∴A1O⊥AC,
∵AC∩BD=O,
∴A1O⊥平面ABC.

∵底面ABCD为菱形,∴AB∥CD,
又∵AA1∩AB=A,CD∩DD1=D,
∴平面AA1BB1∥平面DC1CD1,
又A1B?平面AA1BB1,CD1?平面DC1CD1,
平面A1BCD1∩平面AA1BB1=A1B,
平面ABCBD1∩平面DC1CD1=D1C,
∴A1B∥B1C,
同理可证:A1D∥B1C.
又∵A1D∩A1B=A1,D1C∩B1C=C,
∴平面A1BC∥平面CD1B1;
(2)∵底面ABCD为菱形,∴AC⊥BD,
又∵AA1⊥BD,AA1∩AC=A,∴DB⊥平面A1AO,
∵A1O?平面A1AO,∴BD⊥A1O,
由∵A1A=A1C,∴A1O⊥AC,
∵AC∩BD=O,
∴A1O⊥平面ABC.
点评:本题考查了空间几何题 的性质,运用判断直线,平面的平行、垂直关系.属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知点An(n,an)(x∈N*)都在函数y=ax(a>0且a≠1)的图象上,则( )
| A、a2+a8>2a5 |
| B、a2+a8<2a5 |
| C、a2+a8=2a5 |
| D、a2+a8与2a5的大小与a有关 |
设U=R全集,集合A={y|y=x2+1},B={x|x2-2x-3≥0},则A∩(∁UB)=( )
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1<x≤1} |
| D、{x|1≤x<3} |
若等比数列{an}的各项均为正数,且a3a8+a5a6=2e5,则lna1+lna2+…+lna10=( )
| A、20 | B、25 | C、30 | D、50 |