题目内容
已知f(x)=
,x∈[2,6].
(1)证明:f(x)是定义域上的减函数;
(2)求f(x)的最大值和最小值.
| 1 |
| x-1 |
(1)证明:f(x)是定义域上的减函数;
(2)求f(x)的最大值和最小值.
考点:函数单调性的判断与证明,函数的最值及其几何意义
专题:函数的性质及应用
分析:本题(1)利用函数的单调性定义证明f(x)是定义域上的减函数,得到本题结论;(2)函数的单调性结合函数的定义域,求出f(x)的最大值和最小值,得到本题结论.
解答:
解:(1)在区间[2,6]上任取x1,x2,且取x1<x2,
则:f(x1)-f(x2)=
-
=
,
∵2<x1<x2<6,
∴x1-1>0,x2-1>0,x2-x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)是定义域上的减函数.
(2)由(1)知:f(x)是定义域上的减函数.
∵x∈[2,6]
∴f(2)≥f(x)≥f(6),
∴
≤f(x)≤1.
∴f(x)的最大值为1,f(x)的最小值为
.
则:f(x1)-f(x2)=
| 1 |
| x1-1 |
| 1 |
| x2-1 |
| x2-x1 |
| (x1+1)(x2+1) |
∵2<x1<x2<6,
∴x1-1>0,x2-1>0,x2-x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)是定义域上的减函数.
(2)由(1)知:f(x)是定义域上的减函数.
∵x∈[2,6]
∴f(2)≥f(x)≥f(6),
∴
| 1 |
| 5 |
∴f(x)的最大值为1,f(x)的最小值为
| 1 |
| 5 |
点评:本题考查了函数的单调性的定义和应用,本题难度不大,属于基础题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
某次国际象棋比赛规定,胜一局得3分,平一局得1分,负一局得0分,某参赛队员比赛一局胜的概率为a,平局的概率为b,负的概率为c(a、b、c∈[0,1)),已知他比赛一局得分的数学期望为1,则ab的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若3a>1,则实数a的取值范围为( )
| A、a<0 | B、0<a<1 |
| C、a>0 | D、a>2 |
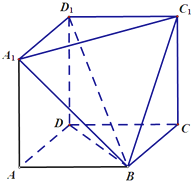 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
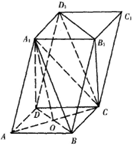 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,O是底面ABCD的对角线的交点,A1A=A1C,A1A⊥BC.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,O是底面ABCD的对角线的交点,A1A=A1C,A1A⊥BC.