题目内容
若等比数列{an}的各项均为正数,且a3a8+a5a6=2e5,则lna1+lna2+…+lna10=( )
| A、20 | B、25 | C、30 | D、50 |
考点:数列的求和
专题:等差数列与等比数列
分析:设等比数列{an}的首项为a1,公比为q,根据已知可得a12q9=e5,从而可求lna1+lna2+…+lna10=lna1×a2×…a10=lna110q1+2+..+9=lne55=25.
解答:
解:设等比数列{an}的首项为a1,公比为q,
a3a8+a5a6=2e5⇒a1q2×a1q7+a1q4a1q5=2e5⇒a12q9=e5
故lna1+lna2+…+lna10=lna1×a2×…a10=lna110q1+2+..+9=lna110q45=ln(a12q9)5=lne55=25
故选:B.
a3a8+a5a6=2e5⇒a1q2×a1q7+a1q4a1q5=2e5⇒a12q9=e5
故lna1+lna2+…+lna10=lna1×a2×…a10=lna110q1+2+..+9=lna110q45=ln(a12q9)5=lne55=25
故选:B.
点评:本题主要考察了等比数列的求和,属于基础题.

练习册系列答案
相关题目
已知函数y=sin(2x+φ)向左平移
个单位,所得函数图象关于y轴对称,则φ的最小正值为( )
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
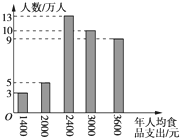 对“小康县”的经济评价标准:
对“小康县”的经济评价标准:①年人均收入不小于7000元;
②年人均食品支出不大于收入的35%.某县有40万人,调查数据如下:
| 年人均收入/元 | 0 | 2000 | 4000 | 6000 | 8000 | 10 000 | 12 000 | 16 000 |
| 人数/万人 | 6 | 3 | 5 | 5 | 6 | 7 | 5 | 3 |
| A、是小康县 |
| B、达到标准①,未达到标准②,不是小康县 |
| C、达到标准②,未达到标准①,不是小康县 |
| D、两个标准都未达到,不是小康县 |
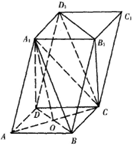 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,O是底面ABCD的对角线的交点,A1A=A1C,A1A⊥BC.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为菱形,O是底面ABCD的对角线的交点,A1A=A1C,A1A⊥BC.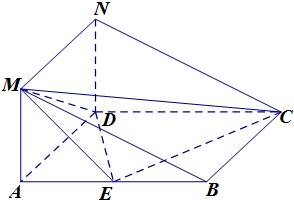 如图所示的几何体中,四边形ABCD是菱形,ADMN是矩形,平面ADMN⊥平面ABCD,∠DAB=
如图所示的几何体中,四边形ABCD是菱形,ADMN是矩形,平面ADMN⊥平面ABCD,∠DAB=