题目内容
7.在如图所示的计算1+5+9+…+2013的程序框图中,判断框内应填入( )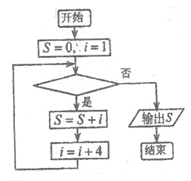
| A. | i≤504 | B. | i≤2009 | C. | i<2013 | D. | i≤2013 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值.
解答 解:程序运行过程中,各变量值如下表所示:
第一圈:S=0+1,i=5,
第二圈:S=1+3,i=9,
第三圈:S=1+3+5,i=13,
…
依此类推,第503圈:1+3+5+…+2013,i=2017,
退出循环,
其中判断框内应填入的条件是:i≤2013,
故选D.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设集合A={x|x2-3x+2>0},B={x|3x-4>0},则A∩B=( )
| A. | (-2,-$\frac{4}{3}$) | B. | (-2,$\frac{4}{3}$) | C. | (1,$\frac{4}{3}$) | D. | (2,+∞) |
19.已知函数f(x)=$\left\{\begin{array}{l}{-\frac{3x+2}{x+1},x∈(-1,0]}\\{x,x∈(0,1]}\end{array}\right.$且g(x)=mx+m,若方程g(x)=f(x)在(-1,1]内有且仅有两个不同的根,则实数m的取值范围是( )
| A. | (-$\frac{11}{4}$,-2]∪(0,$\frac{1}{2}$] | B. | (-$\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$] | C. | (-$\frac{11}{4}$,-2]∪(0,$\frac{2}{3}$] | D. | (-$\frac{9}{4}$,-2]∪(0,$\frac{2}{3}$] |
16.设变量x,y满足不等式$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |