题目内容
17.已知抛物线C:x2=2py(p>0),P,Q是C上任意两点,点M(0,-1)满足$\overrightarrow{MP}•\overrightarrow{MQ}≥0$,则p的取值范围是(0,2].分析 过G作抛物线的切线,根据导数的几何意义,求得k=±$\sqrt{\frac{2}{p}}$,只需令切线的夹角小于90°即可,则$\sqrt{\frac{2}{p}}$≥1,即可求得p的取值范围.
解答 解:过G点作抛物线的两条切线,设切线方程为y=kx-1,
切点坐标为M(x0,y0),N(-x0,y0),
由y=$\frac{{x}^{2}}{2p}$,y′=$\frac{1}{p}$x,
则由导数的几何意义可知$\left\{\begin{array}{l}{{x}_{0}^{2}={2py}_{0}}\\{{y}_{0}=k{x}_{0}-1}\\{\frac{{x}_{0}}{p}=k}\end{array}\right.$,解得k=±$\sqrt{\frac{2}{p}}$.
$\overrightarrow{MP}•\overrightarrow{MQ}≥0$恒成立,∠AOB≤90°,即∠AGO≤45°,
∴|k|>tan45°=1,即$\sqrt{\frac{2}{p}}$≥1,
解得p≤2,
由p>0,则0<p≤2,
p的取值范围:(0,2],
故答案为:(0,2].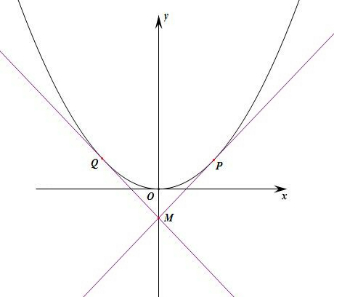
点评 本题考查了直线与抛物线的位置关系,导数的几何意义,考查的数量积,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
8.设F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,点F1到双曲线渐近线的距离为$\frac{\sqrt{2}}{2}$|OF1|(O为坐标原点),则该双曲线的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
6.由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
(Ⅰ)写出m,n的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为ξ,求ξ的分布列和数学期望.
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 2 |
| E | 9500≤x<10500 | n |
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为ξ,求ξ的分布列和数学期望.
7.在如图所示的计算1+5+9+…+2013的程序框图中,判断框内应填入( )
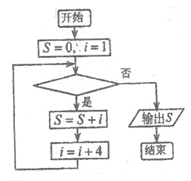

| A. | i≤504 | B. | i≤2009 | C. | i<2013 | D. | i≤2013 |