题目内容
已知函数f(x)=x2-2x+2.
(Ⅰ)求f(x)在区间[
,3]上的最大值和最小值;
(Ⅱ)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
(Ⅰ)求f(x)在区间[
| 1 |
| 2 |
(Ⅱ)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:(1)根据f(x)=x2-2x+2=(x-1)2+1,x∈[
,3],再利用二次函数的性质求得f(x)在区间[
,3]上的最值.
(2)根据g(x)=f(x)-mx=x2-(m+2)x+2在[2,4]上是单调函数,可得
≤2,或
≥4,由此求得m的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据g(x)=f(x)-mx=x2-(m+2)x+2在[2,4]上是单调函数,可得
| m+2 |
| 2 |
| m+2 |
| 2 |
解答:
解:(1)∵f(x)=x2-2x+2=(x-1)2+1,x∈[
,3],
∴f(x)的最小值是f(1)=1,f(x)的最大值是f(3)=5,
即f(x)在区间[
,3]上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2
,∴
≤2,或
≥4,
解得m≤2或m≥6,
故m的取值范围是(-∞,2]∪[6,+∞).
| 1 |
| 2 |
∴f(x)的最小值是f(1)=1,f(x)的最大值是f(3)=5,
即f(x)在区间[
| 1 |
| 2 |
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2
,∴
| m+2 |
| 2 |
| m+2 |
| 2 |
解得m≤2或m≥6,
故m的取值范围是(-∞,2]∪[6,+∞).
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
全集U=R,集合A={x|2>2x-1≥1},集合B={x|y=ln(1-x)},则A∩(∁UB)=( )
| A、[1,2] |
| B、(1,2] |
| C、[1,2) |
| D、(-∞,2] |
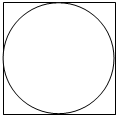 如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )
如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )A、1-
| ||
| B、π | ||
C、
| ||
D、1-
|
已知锐角△ABC的面积为3,BC=4,CA=3,则角C的大小为( )
| A、75° | B、60° |
| C、45° | D、30° |
到点A(1,1,1)、B(-1,-1,-1)的距离相等的点C(x,y,z)的坐标满足( )
| A、x+y+z=-1 |
| B、x+y+z=0 |
| C、x+y+z=1 |
| D、x+y+z=3 |