题目内容
4.已知函数f(x)为偶函数,且在[0,+∞)上单调递增,f(-3)=0,则满足f(x2-x+1)>0的x的取值范围为(-∞,-1)∪(2,+∞).分析 根据题意,由于函数f(x)为偶函数,则有f(3)=f(-3)=0,结合函数在[0,+∞)上单调递增,则f(x2-x+1)>0可以变形为|x2-x+1|>3,解可得x的取值范围,即可得答案.
解答 解:根据题意,函数f(x)为偶函数,则f(3)=f(-3)=0,
又由函数f(x)在[0,+∞)上单调递增,则f(x2-x+1)>0可以变形为|x2-x+1|>3,
即x2-x-2>0,
解可得x>2或x<-1,
即x的取值范围为(-∞,-1)∪(2,+∞).
点评 本题考查函数奇偶性与单调性的综合应用,关键是将f(x2-x+1)>0转化为关于x的不等式.

练习册系列答案
相关题目
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,第二象限的点P(x0,y0)满足bx0+ay0=0,若|PF1|:|PF2|:|F1F2|=1:$\sqrt{3}$:2,则双曲线C的离心率为( )
| A. | $\sqrt{5}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
13.已知抛物线关于y轴对称,顶点在原点,且过点M(x0,3),点M到焦点的距离为4,则OM(O为坐标原点)等于( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{21}$ | C. | $\frac{\sqrt{45}}{2}$ | D. | 21 |
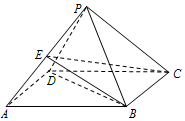 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA=$\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA=$\sqrt{6}$.