题目内容
1.已知函数f(x)=axln(x+1)+x+1(x>-1,a∈R).(1)若$a=\frac{1}{e}$,求函数f(x)的单调区间;
(2)当x≥0时,不等式f(x)≤ex恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)记g(x)=f(x)-ex(x≥0),g(0)=0,求出函数的导数,记h(x)=a[ln(x+1)+1-$\frac{1}{x+1}$]+1-ex,通过讨论a的范围,求出函数的单调性,从而确定a的具体范围即可.
解答 解:(1)a=$\frac{1}{e}$时,f(x)=$\frac{1}{e}$xln(x+1)+x+1,
f′(x)=$\frac{1}{e}$[ln(x+1)+1-$\frac{1}{x+1}$]+1,
∵f′(x)在(-1,+∞)递增,且f′(-1+$\frac{1}{e}$)=0,
故x∈(-1,-1+$\frac{1}{e}$)时,f′(x)<0,f(x)递减,
x∈(-1+$\frac{1}{e}$,+∞)时,f′(x)>0,f(x)递减,
故f(x)在(-1,-1+$\frac{1}{e}$)递减,在(-1+$\frac{1}{e}$,+∞);
(2)记g(x)=f(x)-ex(x≥0),g(0)=0,
则g′(x)=a[ln(x+1)+1-$\frac{1}{x+1}$]+1-ex,
记h(x)=a[ln(x+1)+1-$\frac{1}{x+1}$]+1-ex,
h′(x)=a[$\frac{1}{{(x+1)}^{2}}$+$\frac{1}{x+1}$]-ex,h′(0)=2a-1,
①a≤$\frac{1}{2}$时,∵$\frac{1}{{(x+1)}^{2}}$+$\frac{1}{x+1}$∈(0,2],ex≥1,
∴h′(x)≤0,h(x)在(0,+∞)递减,
则h(x)≤h(0)=0,即g′(x)≤0,∴g(x)在(0,+∞)递减,
∴g(x)≤g(0)=0恒成立,即f(x)≤ex恒成立,满足题意;
②a≥$\frac{1}{2}$时,h′(x)在(0,+∞)递减,
又h′(0)=2a-1>0,x→+∞时,h′(x)→-∞,
则必存在x0∈(0,+∞),使得h′(x0)=0,
则x∈(0,x0)时,h′(x)>0,h(x)在(0,x0)递增,
此时h(x)>h(0)=0,
x∈(0,x0)时,g′(x)>0,∴g(x)在(0,x0)递增,
∴g(x)>g(0)=0,即f(x)>ex,不合题意,
综上,a≤$\frac{1}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.

| A. | $({-\frac{1}{2},+∞})$ | B. | (0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
| A. | (0,1) | B. | (-1,2) | C. | (-1,1) | D. | (-∞,-1]∪[2,+∞) |
| A. | -1 | B. | 1 | C. | -$\frac{1}{3}$ | D. | $-\frac{2}{3}$ |
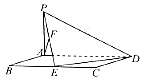 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥平面ABCD,PA=2,E,F分别为BC,PE的中点.