题目内容
19.已知cosx-sinx=$\frac{3\sqrt{2}}{5}$,则$\frac{cos2x}{sin(x+\frac{π}{4})}$=$\frac{6}{5}$.分析 利用二倍角公式以及两角和的正弦函数化简所求表达式,然后求解即可.
解答 解:cosx-sinx=$\frac{3\sqrt{2}}{5}$,则$\frac{cos2x}{sin(x+\frac{π}{4})}$=$\frac{co{s}^{2}x-si{n}^{2}x}{\frac{\sqrt{2}}{2}(sinx+cosx)}$=$\sqrt{2}$(cosx-sinx)=$\frac{3\sqrt{2}}{5}×\sqrt{2}$=$\frac{6}{5}$.
故答案为:$\frac{6}{5}$.
点评 本题考查三角函数的化简求值,二倍角公式以及两角和的正弦函数的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知线段PQ两端点的坐标分别为(-1,1),(2,2),若直线l:x+my+m=0与线段PQ有交点,则m的范围是( )
| A. | $(-∞,-\frac{2}{3}]∪[\frac{1}{2},+∞)$ | B. | $[-\frac{2}{3},\frac{1}{2}]$ | C. | $(-∞,-\frac{3}{2}]∪[2,+∞)$ | D. | $[-\frac{3}{2},2]$ |
7.若y=f(x)在(-∞,+∞)可导,且$\lim_{△x→0}\frac{f(a+2△x)-f(a)}{3△x}=1$,则f′(a)=( )
| A. | $\frac{2}{3}$ | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
14.某产品的广告费x(万元)与销售额y(万元)的统计数据如表:
根据如表可知回归直线方程$\stackrel{∧}{y}$=7x+$\stackrel{∧}{a}$,若广告费用为10万元,则预计销售额为73.5万元.
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
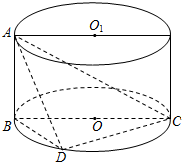 如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.
如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.