Question

9．已知函数f（x）是实数集R上的奇函数，当x＞0时，f（x）=x²+x．
（1）求f（-1）的值；
（2）求函数f（x）的表达式；
（3）解不等式：f（2x-1）＜f（1）．

Answer 1

分析 （1）根据函数奇偶性的性质即可求f（-1）的值；
（2）结合函数奇偶性的性质利用对称性即可求函数f（x）的表达式；
（3）判断函数的单调性，利用函数的单调性即可解不等式．

解答 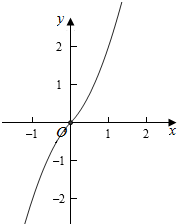解：（1）∵函数f（x）是实数集R上的奇函数，当x＞0时，f（x）=x²+x，
∴f（-1）=-f（1）=-（1+1）=-2；
（2）∵函数f（x）是实数集R上的奇函数，当x＞0时，f（x）=x²+x，
∴f（0）=0，
若x＜0，则-x＞0，
则f（-x）=x²-x=-f（x），
则f（x）=-x²+x，x＜0，
则函数f（x）的表达式为f（x）=$\left\{\begin{array}{l}{{x}^{2}+x，}&{x≥0}\\{-{x}^{2}+x，}&{x＜0}\end{array}\right.$；
（3）作出函数f（x）的图象如图：
则函数在（-∞，+∞）上为增函数，
则解不等式：f（2x-1）＜f（1）等价为2x-1＜1．
得x＜1，
即不等式的解集为（-∞，1）．

点评 本题主要考查函数解析式的求解以及函数奇偶性的应用，利用函数奇偶性和单调性的性质是解决本题的关键．