题目内容
10.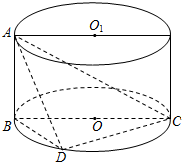 如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.
如图所示,圆柱O1O中,母线AB与底面垂直,BC是⊙O的直径,点D是⊙O的圆周上异于B,C的点.(1)求证:平面ABD⊥平面ADC;
(2)若BD=2,CD=4,AC=6,求圆柱O1O的表面积.
分析 (1)推导出AB⊥CD,BD⊥CD,从而CD⊥平面ABD,由此能证明平面ABD⊥平面ADC.
(2)由勾股定理求出BC,AB,由此能求出圆柱O1O的表面积.
解答  证明:(1)由已知可知AB⊥平面BCD,CD?平面BCD,
证明:(1)由已知可知AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD…(1分)
∵点D是⊙O的圆周上异于异于B,C的点,BC是⊙O的直径,
∴∠BDC是直角,即BD⊥CD…(2分)
又∵AB?平面ABD,BD?平面ABD,AB∩BD=B,
∴CD⊥平面ABD,…(4分)
∵CD?平面ADC,
∴平面ABD⊥平面ADC.…(6分)
解:(2)在Rt△BCD中,BD=2,CD=4,∠BDC=90°,
∴$BC=\sqrt{B{D^2}+C{D^2}}=\sqrt{{2^2}+{4^2}}=2\sqrt{5}$,…(8分)
由(1)知AB⊥平面BCD,BC?平面BCD,
∴AB⊥BC,即∠ABC=90°
∴$AB=\sqrt{A{C^2}-B{C^2}}=\sqrt{{6^2}-{{(2\sqrt{5})}^2}}=4$…(10分)
∴圆柱O1O的表面积为:
S表=S侧+2S底=$2π•\frac{BC}{2}•AB+2π•{(\frac{BC}{2})^2}$=$(8\sqrt{5}+10)π$.…(14分)
点评 本题考查面面垂直的证明,考查圆柱的表面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
1.已知函数f(x)=loga(x-m)的图象过点(4,0)和(7,1),则f(x)在定义域上是( )
| A. | 增函数 | B. | 减函数 | C. | 奇函数 | D. | 偶函数 |
18.设函数g(x)=x(x2-1),则g(x)在区间[0,1]上的最小值为( )
| A. | -1 | B. | 0 | C. | -$\frac{2\sqrt{3}}{9}$ | D. | $\frac{\sqrt{3}}{3}$ |
5.设全集U={-2,-1,0,1,2},集合A={x|x2-x-2=0},B={1,2},则(∁UA)∪B=( )
| A. | {-2,-1,0,1,2} | B. | {-2,0,1,2} | C. | {-1,2} | D. | {-1,1,2} |