题目内容
9.已知线段PQ两端点的坐标分别为(-1,1),(2,2),若直线l:x+my+m=0与线段PQ有交点,则m的范围是( )| A. | $(-∞,-\frac{2}{3}]∪[\frac{1}{2},+∞)$ | B. | $[-\frac{2}{3},\frac{1}{2}]$ | C. | $(-∞,-\frac{3}{2}]∪[2,+∞)$ | D. | $[-\frac{3}{2},2]$ |
分析 (方法一)利用直线l过定点,结合图象,看斜率与已知直线斜率间的关系,列出不等式解出m的范围.
(方法二)由题意知,P,Q两点在直线的两侧或其中一点在直线l上,故有(-1+m+m)•(2+2m+m)≤0
解答 解:(方法一)直线l:x+my+m=0恒过A(0,-1)点,
kAP=$\frac{-1-1}{0+1}$=-2,kAQ=$\frac{-1-2}{0-2}$=$\frac{3}{2}$,
则-$\frac{1}{m}$≥$\frac{3}{2}$或-$\frac{1}{m}$≤-2,∴-$\frac{2}{3}$≤m≤$\frac{1}{2}$且m≠0,
又∵m=0时直线l:x+my+m=0与线段PQ有交点,
∴所求m的范围是-$\frac{2}{3}$≤m≤$\frac{1}{2}$;
(方法二)∵P,Q两点在直线的两侧或其中一点在直线l上,
∴(-1+m+m)•(2+2m+m)≤0解得:-$\frac{2}{3}$≤m≤$\frac{1}{2}$,
∴所求m的范围是-$\frac{2}{3}$≤m≤$\frac{1}{2}$;
故选:B.
点评 本题考查2条直线的交点问题,借助图形,增强了直观性,容易找到简单正确的解题方法,体现了数形结合的数学思想.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
17.2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:
现从该港口随机抽取了n家公司,其中消防安全等级为三级的恰有20家.
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
| 等 级 | 一级 | 二级 | 三级 | 四级 |
| 频 率 | 0.30 | 2m | m | 0.10 |
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
1.已知函数f(x)=loga(x-m)的图象过点(4,0)和(7,1),则f(x)在定义域上是( )
| A. | 增函数 | B. | 减函数 | C. | 奇函数 | D. | 偶函数 |
18.设函数g(x)=x(x2-1),则g(x)在区间[0,1]上的最小值为( )
| A. | -1 | B. | 0 | C. | -$\frac{2\sqrt{3}}{9}$ | D. | $\frac{\sqrt{3}}{3}$ |
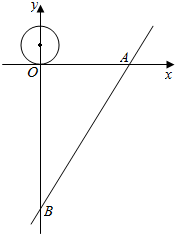 如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.
如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.