题目内容
求平行于x+y+9=0且被圆x2+y2=25截得弦长为5
的弦所在的直线方程.
| 2 |
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:设所求直线方方程为x+y+c=0,利用直线被圆x2+y2=25截得弦长为5
,可得
+(
)2=25,即可求出直线方程.
| 2 |
| c2 |
| 2 |
5
| ||
| 2 |
解答:
解:设所求直线方方程为x+y+c=0,则,
∵直线被圆x2+y2=25截得弦长为5
,
∴
+(
)2=25,
∴c=±5,
∴所求直线方方程为x+y±5=0.
∵直线被圆x2+y2=25截得弦长为5
| 2 |
∴
| c2 |
| 2 |
5
| ||
| 2 |
∴c=±5,
∴所求直线方方程为x+y±5=0.
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,勾股定理,垂径定理,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
已知定义在R上的函数f(x)满足:对于任意实数x、y,恒有f(x)f(y)=f(x+y),且f(1)=2,则f(10)=( )
| A、256 | B、512 |
| C、1024 | D、2048 |
下列函数中,最小值等于2的函数是( )
A、y=x+
| ||||
B、y=
| ||||
| C、y=ex+4e-x-2 | ||||
D、y=cosx+
|
若log23=
,则3x=( )
| 1 |
| x |
| A、1 | B、3 |
| C、log23 | D、2 |
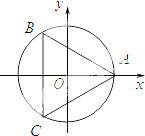 如图,在单位圆中,用三角形的重心公式
如图,在单位圆中,用三角形的重心公式