题目内容
已知定义在R上的函数f（x）满足：对于任意实数x、y，恒有f（x）f（y）=f（x+y），且f（1）=2，则f（10）=（ ）
| A、256 | B、512 |
| C、1024 | D、2048 |
考点：抽象函数及其应用
专题：计算题,函数的性质及应用
分析：由f（x）f（y）=f（x+y）反复应用可得f（10）=f（1）10=210=1024．
解答：
解：由f（x）f（y）=f（x+y）可得，
f（10）=f（9）f（1）=f（8）f（1）2=…
=f（1）10=210=1024，
故选C．
f（10）=f（9）f（1）=f（8）f（1）2=…
=f（1）10=210=1024，
故选C．
点评：本题考查了学生对新知识的接受能力，属于中档题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
点P为椭圆
+
=1上一点，以点P以及焦点F1、F2为顶点的三角形的面积为1，则P点的坐标为（ ）
| x2 |
| 5 |
| y2 |
| 4 |
A、（±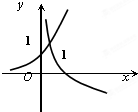
| ||||
B、（
| ||||
C、（
| ||||
D、（±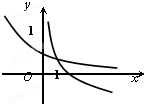
|
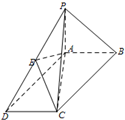如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．当a＞1时，在同一坐标系中，函数y=a-x与y=logax的图象为（ ）
A、 |
B、 |
C、 |
D、 |