题目内容
已知cosα=
,α∈(-
,0),求cos(
-α)的值.
| 4 |
| 5 |
| π |
| 2 |
| π |
| 3 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由题意和同角三角函数的基本关系可得sinα=-
,而cos(
-α)=
cosα+
sinα,代值计算可得.
| 3 |
| 5 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
解答:
解:∵cosα=
,α∈(-
,0),
∴sinα=-
=-
,
∴cos(
-α)=
cosα+
sinα
=
×
+
×(-
)=
.
| 4 |
| 5 |
| π |
| 2 |
∴sinα=-
| 1-cos2α |
| 3 |
| 5 |
∴cos(
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
4-3
| ||
| 10 |
点评:本题考查两角和与差的余弦函数,涉及同角三角函数的基本关系,属基础题.

练习册系列答案
相关题目
点P为椭圆
+
=1上一点,以点P以及焦点F1、F2为顶点的三角形的面积为1,则P点的坐标为( )
| x2 |
| 5 |
| y2 |
| 4 |
A、(±
| ||||
B、(
| ||||
C、(
| ||||
D、(±
|
已知A,B在抛物线y2=2px(p>0)上,O为坐标原点,如果|OA|=|OB|且△AOB的重心恰好是此抛物线的焦点F,则AB直线的方程是( )
| A、x-p=0 |
| B、4x-3p=0 |
| C、2x-5p=0 |
| D、2x-5p=0 |
 如图,在△ABC中,点D、E分别在边BC、C上,且BD=
如图,在△ABC中,点D、E分别在边BC、C上,且BD=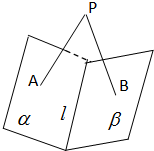 如图,p是二面角α-l-β内的一点(p∉α,p∉β),PA⊥α于点A,PB⊥β于点B,∠APB=35°,则二面角α-l-β的大小是
如图,p是二面角α-l-β内的一点(p∉α,p∉β),PA⊥α于点A,PB⊥β于点B,∠APB=35°,则二面角α-l-β的大小是