题目内容
8.命题$p:?x∈(0,\frac{π}{2}),f(x)<0$,则?p:$?x∈(0,\frac{π}{2}),f(x)≥0$.分析 直接利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题$p:?x∈(0,\frac{π}{2}),f(x)<0$,则?p:$?x∈(0,\frac{π}{2}),f(x)≥0$.
故答案为:$?x∈(0,\frac{π}{2}),f(x)≥0$
点评 本题考查命题得到,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
3.sin18°•sin78°-cos162°•cos78°等于( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
13.一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是( )
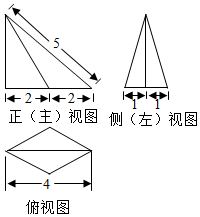

| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
20.运行下面的程序框图,输出的结果为( )
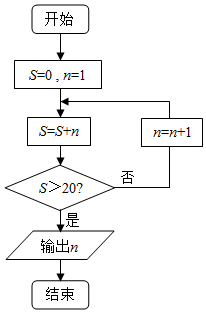

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
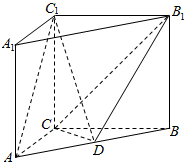 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.