题目内容
20.运行下面的程序框图,输出的结果为( )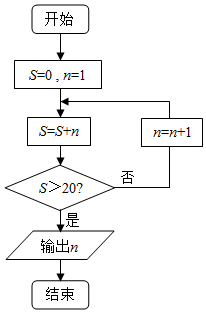
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 模拟执行程序框图,依次写出每次循环得到的S,n的值,当S=21时,满足条件S>20,退出循环,输出n的值为6.
解答 解:模拟执行程序框图,可得
S=0,n=1
S=1,
不满足条件S>20,n=2,S=3
不满足条件S>20,n=3,S=6
不满足条件S>20,n=4,S=10
不满足条件S>20,n=5,S=15
不满足条件S>20,n=6,S=21
满足条件S>20,退出循环,输出n的值为6.
故选:B.
点评 本题主要考查了循环结构的程序框图和算法,正确依次写出每次循环得到的S,k的值是解题的关键,属于基本知识的考查.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
3.已知:幂函数y=x3m-7(m∈N*)在区间(0,+∞)内为减函数,且幂函数的图象关于y轴对称,则m等于( )
| A. | -4 | B. | 1或2 | C. | 1 | D. | 2 |
5.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3),若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥$\overrightarrow{a}$,$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | (-$\frac{7}{4}$,$\frac{7}{8}$) | B. | ($\frac{7}{2}$,-$\frac{7}{4}$) | C. | (-$\frac{7}{2}$,-$\frac{7}{4}$) | D. | (-$\frac{7}{2}$,$\frac{7}{4}$) |
12.已知集合A={-1,0,1},B={y|y=x2-x,x∈A},则A∩B=( )
| A. | ?{0}? | B. | {2} | C. | ?{0,1}? | D. | {-1,0} |
9.已知直线l:y=kx与椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$交于A、B两点,其中右焦点F的坐标为(c,0),且AF与BF垂直,则椭圆C的离心率的取值范围为( )
| A. | $[{\frac{{\sqrt{2}}}{2},1})$ | B. | $({0,\frac{{\sqrt{2}}}{2}}]$ | C. | $({\frac{{\sqrt{2}}}{2},1})$ | D. | $({0,\frac{{\sqrt{2}}}{2}})$ |
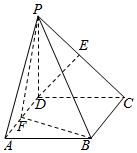 四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.
四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.