题目内容
13.一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是( )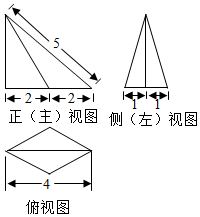
| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
分析 根据三视图得出底面积和棱锥的高,代入体积计算.
解答 解:由三视图的数量关系可知俯视图菱形的对角线长分别为4和2,
∴棱锥的底面菱形的面积为S=$\frac{1}{2}×2×4=4$.
由主视图可知棱锥的高为h=$\sqrt{{5}^{2}-{4}^{2}}=3$.
∴棱锥的体积V=$\frac{1}{3}Sh$=$\frac{1}{3}×4×3=4$.
故选B.
点评 本题考查了棱锥的结构特征,三视图,体积计算,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3),若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥$\overrightarrow{a}$,$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | (-$\frac{7}{4}$,$\frac{7}{8}$) | B. | ($\frac{7}{2}$,-$\frac{7}{4}$) | C. | (-$\frac{7}{2}$,-$\frac{7}{4}$) | D. | (-$\frac{7}{2}$,$\frac{7}{4}$) |
2.在空间,下列说法正确的是( )
| A. | 两组对边相等的四边形是平行四边形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 平行于同一直线的两条直线平行 | |
| D. | 三点确定一个平面 |
3.已知椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的右焦点为F,P是椭圆上一点,点$A({0,2\sqrt{3}})$,当△APF的周长最大时,△APF的面积等于( )
| A. | $\frac{{11\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{21}{4}$ |
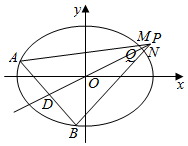 如图,已知直线OP交椭圆C:$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1于点Q,其中O为坐标原点,点P的坐标为(2,1),$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$,若椭圆C不经过原点的弦AB被直线OP平分于点D,且直线AP,BP与椭圆C的另一交点分别为M,N.
如图,已知直线OP交椭圆C:$\frac{{x}^{2}}{4{m}^{2}}$+$\frac{{y}^{2}}{3{m}^{2}}$=1于点Q,其中O为坐标原点,点P的坐标为(2,1),$\overrightarrow{OQ}$=$\frac{\sqrt{3}}{2}$$\overrightarrow{OP}$,若椭圆C不经过原点的弦AB被直线OP平分于点D,且直线AP,BP与椭圆C的另一交点分别为M,N.