题目内容
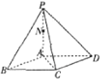 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点N是PA的中点,且PA=AB=2,点O是△PCD内(含边界)一动点,则三棱锥O-ADN的体积不小于
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点N是PA的中点,且PA=AB=2,点O是△PCD内(含边界)一动点,则三棱锥O-ADN的体积不小于
| ||
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:常规题型,概率与统计
分析:分析可知,概率比应等于面积比.
解答:
解:设O到平面ADN的距离为h,当三棱锥O-ADN的体积等于
时,
hS△ADN=
,
∵S△ADN=1,∴h=
,
∵C到AD的距离为
.
∴点O在图中线段FG上,且FG∥PD.
∴F是CD的中点,此时点O在三角面CFG内运动,
∴三棱锥O-ADN的体积不小于
的概率P=
.
故选:D.
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
∵S△ADN=1,∴h=
| ||
| 2 |
∵C到AD的距离为
| 3 |
∴点O在图中线段FG上,且FG∥PD.
∴F是CD的中点,此时点O在三角面CFG内运动,
∴三棱锥O-ADN的体积不小于
| ||
| 6 |
| 1 |
| 4 |
故选:D.
点评:本题考查了几何概型,注意动点构成的是面积.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
下列说法中正确的是( )
| A、若直线m与平面α内的无数条直线平行,则m∥α |
| B、若m∥α,n?α,则m与n的位置关系是平行或异面 |
| C、若β∥α,m∥α,则m∈β |
| D、若m∥α,n∥α,则m∥n |
已知函数f(x)=x2-4x+c,p=f(1),q=f(4),r=f(-2),则p,q,r的大小关系是( )
| A、r>p>q |
| B、q>p>r |
| C、r>q>p |
| D、q>r>p |
已知命题p:?∈(1,+∞),函数f(x)=log2(x+1)-1有零点;命题q:“a=-1”是“直线(a-1)x+2y=0与直线x-ay+1=0垂直”的充分必要条件,则下列命题为真命题的是( )
| A、p∧q |
| B、p∨(¬q) |
| C、(¬p)∧q |
| D、p∧(¬q) |
不等式
<1的解集为( )
| 1 |
| x |
| A、(1,+∞) |
| B、(-∞,0)∪(1,+∞) |
| C、(-∞,0) |
| D、(-∞,-1)∪(1,+∞) |
下列命题中正确的是( )
(1)已知a,b∈R,则a=b是(a-b)+(a+b)i为纯虚数的充要条件
(2)当z是非零实数时,|z+
|≥2恒成立
(3)复数z=(1-i)3的实部和虚部都是-2
(4)设z的共轭复数为
,若z+
=4,z•
=8,则
=-i.
(1)已知a,b∈R,则a=b是(a-b)+(a+b)i为纯虚数的充要条件
(2)当z是非零实数时,|z+
| 1 |
| z |
(3)复数z=(1-i)3的实部和虚部都是-2
(4)设z的共轭复数为
. |
| z |
. |
| z |
. |
| z |
| ||
| z |
| A、(1)(2) |
| B、(1)(3) |
| C、(2)(3) |
| D、(2)(4) |