题目内容
已知命题p:?∈(1,+∞),函数f(x)=log2(x+1)-1有零点;命题q:“a=-1”是“直线(a-1)x+2y=0与直线x-ay+1=0垂直”的充分必要条件,则下列命题为真命题的是( )
| A、p∧q |
| B、p∨(¬q) |
| C、(¬p)∧q |
| D、p∧(¬q) |
考点:复合命题的真假
专题:简易逻辑
分析:先判断出命题p,q的真假,然后根据连接词∧,∨,¬所构成的复合命题和原命题p或q真假的关系,判断每个选项下的命题的真假.
解答:
解:命题p:x∈(1,+∞)时,x+1>2,∴log2(x+1)>log22=1,∴f(x)>0;
∴函数f(x)在(1,+∞)上没有零点,∴命题p是假命题;
命题q:a=0时,这两条直线可分别变成,y=
x,x=-1,显然这两直线不垂直;
a≠0时,这两条直线的斜率分别为:
,
,∴这两直线若垂直,则斜率需满足:
•
=-1,∴a=-1;
∴a=-1是这两直线垂直的充要条件;
∴命题q是真命题;
∴p∧q为假命题,¬q为假命题,p∨(¬q)为假命题,¬p是真命题,(¬p)∧q是真命题,p∧(¬q)是假命题;
故选:C.
∴函数f(x)在(1,+∞)上没有零点,∴命题p是假命题;
命题q:a=0时,这两条直线可分别变成,y=
| 1 |
| 2 |
a≠0时,这两条直线的斜率分别为:
| 1-a |
| 2 |
| 1 |
| a |
| 1-a |
| 2 |
| 1 |
| a |
∴a=-1是这两直线垂直的充要条件;
∴命题q是真命题;
∴p∧q为假命题,¬q为假命题,p∨(¬q)为假命题,¬p是真命题,(¬p)∧q是真命题,p∧(¬q)是假命题;
故选:C.
点评:考查对数函数的单调性,函数的零点的概念,两直线相互垂直的充要条件,由∧,∨,¬连接的命题的真假情况.

练习册系列答案
相关题目
若直线x=3的倾斜角为α,则α=( )
| A、0° | B、45° |
| C、90° | D、不存在 |
sin
的值等于( )
| 11π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f(x)=lnx+2x-6有唯一零点,其零点的范围是( )
| A、(1,2) |
| B、(1.5,2) |
| C、(2,3) |
| D、(3,4) |
平行线3x-4y-3=0和6x-8y+5=0之间的距离是( )
A、
| ||
B、
| ||
C、
| ||
D、
|




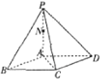 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点N是PA的中点,且PA=AB=2,点O是△PCD内(含边界)一动点,则三棱锥O-ADN的体积不小于
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点N是PA的中点,且PA=AB=2,点O是△PCD内(含边界)一动点,则三棱锥O-ADN的体积不小于