题目内容
不等式
＜1的解集为（ ）
| 1 |
| x |
| A、（1，+∞） |
| B、（-∞，0）∪（1，+∞） |
| C、（-∞，0） |
| D、（-∞，-1）∪（1，+∞） |
考点：其他不等式的解法
专题：计算题,不等式的解法及应用
分析：由
＜1，得
，或
，解出即可．
| 1 |
| x |
|
|
解答：
解：∵
＜1，
∴
＜0，
∴
，或
，
解得：x＜0，或x＞1，
故选：B．
| 1 |
| x |
∴
| 1-x |
| x |
∴
|
|
解得：x＜0，或x＞1，
故选：B．
点评：本题考察了不等式的解法，将不等式转化为不等式组是解题的关键，本题是一道基础题．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
复数Z与点Z对应，Z1，Z2为两个给定的复数，Z1≠Z2，则|Z-Z1|=|Z-Z2|决定的Z的轨迹是（ ）
| A、过Z1，Z2的直线 |
| B、线段Z1Z2的中垂线 |
| C、双曲线的一支 |
| D、以Z1，Z2为端点的圆 |
已知函数f（x）是偶函数，且在区间[1，2]单调递减，则f（x）在区间[-2，-1]上是（ ）
| A、单调递减函数，且有最小值f（1） |
| B、单调递增函数，且有最大值f（1） |
| C、单调递减函数，且有最小值f（2） |
| D、单调递增函数，且有最大值f（2） |
函数f（x）=lnx+2x-6有唯一零点，其零点的范围是（ ）
| A、（1，2） |
| B、（1.5，2） |
| C、（2，3） |
| D、（3，4） |
已知⊙O的半径为r，圆心O到直线l的距离为d，则“d=r”是“直线l与⊙O相切”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
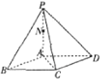如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点N是PA的中点，且PA=AB=2，点O是△PCD内（含边界）一动点，则三棱锥O-ADN的体积不小于
| ||
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、64+
| ||
B、64-
| ||
| C、96 | ||
| D、32 |